题目内容
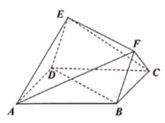
【题目】如图所示多面体![]() ,其底面
,其底面![]() 为矩形且
为矩形且![]() ,四边形
,四边形![]() 为平行四边形,点
为平行四边形,点![]() 在底面
在底面![]() 内的投影恰好是
内的投影恰好是![]() 的中点.
的中点.
(1)已知![]() 为线段
为线段![]() 的中点,证明:
的中点,证明:![]() 平面
平面![]() ;
;
(2)若二面角![]() 大小为
大小为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连结![]() 交
交![]() 于
于![]() ,连结
,连结![]() 由三角形中位线定理可得,
由三角形中位线定理可得,![]() 可得
可得![]() 平面
平面![]() ,可证明
,可证明![]() 平面
平面![]() ,从而平面
,从而平面![]() 平行于平面
平行于平面![]() 平面
平面![]() ;(2)以
;(2)以![]() 的中点
的中点![]() 为原点,以
为原点,以![]() 、
、![]() 的垂直平分线、
的垂直平分线、![]() 为坐标轴,建立如空间直角坐标系,设
为坐标轴,建立如空间直角坐标系,设![]() ,求出平面
,求出平面![]() 的法向量与平面
的法向量与平面![]() 的法向量,由二面角
的法向量,由二面角![]() 大小为
大小为![]() ,利用空间向量夹角余弦公式求出
,利用空间向量夹角余弦公式求出![]() ,求出
,求出![]() 的坐标,由夹角公式可得结果.
的坐标,由夹角公式可得结果.
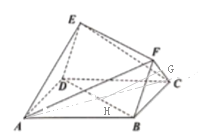
(1)连结![]() 交
交![]() 于
于![]() ,连结
,连结![]() 为
为![]() 的中位线,
的中位线,
![]()
![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() 平面
平面![]() .
.
又知![]() 平面
平面![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 相交,
相交,![]() 由它们确定的平面
由它们确定的平面![]() 平行于平面
平行于平面![]()
![]() 平面
平面![]() 平面
平面![]() .
.
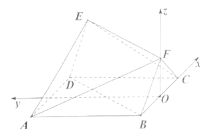
(2)以![]() 的中点
的中点![]() 为原点,以
为原点,以![]() 的垂直平分线、
的垂直平分线、![]() 为坐标轴,建立如图所示空间直角坐标系,设
为坐标轴,建立如图所示空间直角坐标系,设![]() ,其余各点分别是:
,其余各点分别是:![]()
,所以![]()
又设平面![]() 的法向量为
的法向量为![]() .
.
由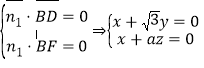
令![]() ,得
,得![]()
易得平面![]() 的法向量为
的法向量为![]()
因为二面角![]() 大小为
大小为![]() .所以由
.所以由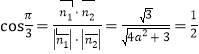 ,
,
解得![]() .
.
![]()
![]() 且
且
![]()
 故直线
故直线![]() 与平面
与平面![]()
所成角的正弦为![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某部门经统计,客户对不同款型理财产品的最满意程度百分比和对应的理财总销售量(万元)如下表(最满意度百分比超高时总销售量最高):
产品款型 | A | B | C | D | E | F | G | H | I | J |
最满意度% | 20 | 34 | 25 | 19 | 26 | 20 | 19 | 24 | 19 | 13 |
总销量(万元) | 80 | 89 | 89 | 78 | 75 | 71 | 65 | 62 | 60 | 52 |
设![]() 表示理财产品最满意度的百分比,
表示理财产品最满意度的百分比,![]() 为该理财产品的总销售量(万元).这些数据的散点图如图所示.
为该理财产品的总销售量(万元).这些数据的散点图如图所示.
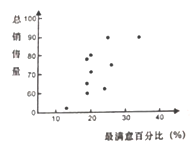
(1)在![]() 份
份![]() 款型理财产品的顾客满意度调查资料中任取
款型理财产品的顾客满意度调查资料中任取![]() 份;只有一份最满意的,求含有最满意客户资料事件的概率.
份;只有一份最满意的,求含有最满意客户资料事件的概率.
(2)我们约定:相关系数的绝对值在![]() 以下是无线性相关,在
以下是无线性相关,在![]() 以上(含
以上(含![]() )至
)至![]() 是一般线性相关,在
是一般线性相关,在![]() 以上(含
以上(含![]() )是较强线性相关,若没有达到较强线性相关则采取“末位”剔除制度(即总销售量最少的那一款产品退出理财销售);试求在剔除“末位”款型后的线性回归方程(系数精确到
)是较强线性相关,若没有达到较强线性相关则采取“末位”剔除制度(即总销售量最少的那一款产品退出理财销售);试求在剔除“末位”款型后的线性回归方程(系数精确到![]() ).
).
数据参考计算值:
项目 |
|
|
|
|
|
|
值 | 21.9 | 72.1 | 288.9 | 37.16 | 452.1 | 17.00 |
附:回归直线方程![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为:
线性相关系数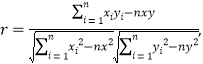
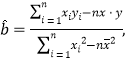
![]() .
.
【题目】郑汴一体化是依托郑州省会城市资源优势发展开封的省级战略,实施至今,取得了一系列的成就:两城电信同价,金融同城,郑开大道全线贯通,城际列车实常态化运营.随着郑汴一体化的深入推进,很多人认为郑州开封未来有望合并.为了解市民对郑汴合并的态度,现随机抽查55人,结果按年龄分类统计形成如下表格:
支持 | 反对 | 合计 | |
不足35岁 | 20 | ||
35岁以上 | 30 | ||
合计 | 25 | 55 |
(1)请完成上面的2×2列联表,并判断是否有99.5%的把握认为市民对郑汴合并的态度与年龄有关?
(2)在上述样木中用分层抽样的方法,从攴持郑汴合并的两组市民中随机抽取6人作进一步调查,从这6人中任选2人,求恰有1位“不足35岁”的市民和1位“35岁及以上”的市民的概率.
附:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.814 | 5.024 | 7.879 | 10.828 |