题目内容
【题目】正三角形
的边长为
，将它沿高
折叠，使点
与点
间的距离为
，则四面体
外接球的表面积为（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
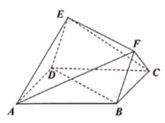
四面体
的三条侧棱BD⊥AD、DC⊥DA，底面是等腰三角形，它的外接球就是它扩展为三棱柱的外接球，求出三棱柱的底面中心连线的中点到顶点的距离，就是球的半径，然后求球的表面积即可．
根据题意可知四面体的三条侧棱BD⊥AD、DC⊥DA，底面是等腰三角形，它的外接球就是它扩展为三棱柱的外接球，求出三棱柱的底面中心连线的中点到顶点的距离，就是球的半径，
三棱柱中，底面△BDC，BD＝CD＝1，BC
，∴∠BDC＝120°，∴△BDC的外接圆的半径为
1
由题意可得：球心到底面的距离为
，
∴球的半径为r
．
外接球的表面积为：4πr2＝7π
故选：B．
练习册系列答案
相关题目
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验，并获得了煤气开关旋钮旋转的弧度数
与烧开一壶水所用时间
的一组数据，且作了一定的数据处理（如下表），得到了散点图（如下图）.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中
，
.
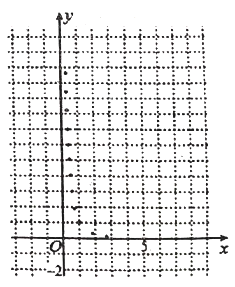
（1）根据散点图判断，
与
哪一个更适宜作烧水时间关于开关旋钮旋转的弧度数的回归方程类型？（不必说明理由）
（2）根据判断结果和表中数据，建立关于的回归方程；
（3）若单位时间内煤气输出量
与旋转的弧度数成正比，那么，利用第（2）问求得的回归方程知为多少时，烧开一壶水最省煤气？
附：对于一组数据
，其回归直线
的斜率和截距的最小二乘法估计值分别为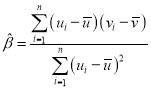
，
