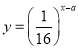题目内容
【题目】已知函数![]()
![]() 1
1![]() 当
当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
![]() 2
2![]() 若关于x的不等式
若关于x的不等式![]() 有实数解,求实数a的取值范围.
有实数解,求实数a的取值范围.
【答案】(Ⅰ)-3<x<-![]() ,(Ⅱ)a>0或a<-4.
,(Ⅱ)a>0或a<-4.
【解析】
(Ⅰ)利用零点法,分类讨论,求出不等式![]() 的解集;
的解集;
(Ⅱ)把不等式![]() ,变形为2|x+2|-x<|x-a|,问题等价于函数y=2|x+2|-x的图象上存在点在函数y=|x-a|的图象下方,画出图象,利用数形结合,求出实数a的取值范围。
,变形为2|x+2|-x<|x-a|,问题等价于函数y=2|x+2|-x的图象上存在点在函数y=|x-a|的图象下方,画出图象,利用数形结合,求出实数a的取值范围。
解:(Ⅰ)当a=1时,f(x)=2|x+1|-|x-1|,
当x<-1时,由f(x)<0得-2(x+1)+(x-1)<0,即-x-3<0,得x>-3,此时-3<x<-1,
当-1≤x≤1,由f(x)<0得2(x+1)+(x-1)<0,即3x+1<0,得x<-![]() ,此时-1≤x<-
,此时-1≤x<-![]() ,
,
当x>1时,由f(x)<0得2(x+1)-(x-1)<0,即x+3<0,得x<-3,此时无解,
综上-3<x<-![]() ,
,
(Ⅱ)∵f(x)<x2|x+2|-x<|x-a|有解,等价于函数y=2|x+2|-x的图象上存在点在函数y=|x-a|的图象下方,
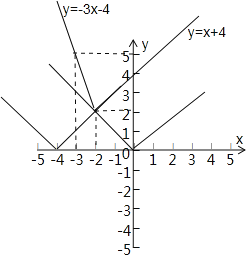
由函数y=2|x+2|-x与函数y=|x-a|的图象可知:a>0或a<-4.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目