题目内容
16.已知f(x)为偶函数,当x≥0时,f(x)=m(|x-2|-1)(m>0),若函数y=f[f(x)]恰有4个零点,则m的取值范围为( )| A. | (0,1) | B. | (1,3) | C. | (1,+∞) | D. | (3,+∞) |
分析 由f(x)的图象为偶函数,图象关于y轴对称,作出图象,令f(x)=0可得x=1,3,-1,-3,然后由y=f[f(x)]=0时可得,f(x)=1或f(x)=3或f(x)=-1,或f(x)=-3,分类讨论m的范围,结合函数的图象可求;
解答 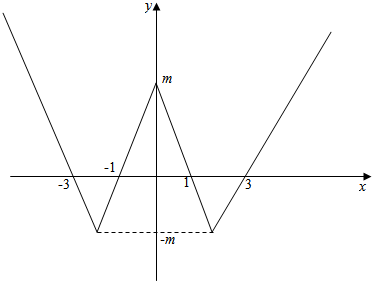 解:x≥0时,f(x)=m(|x-2|-1)(m>0),
解:x≥0时,f(x)=m(|x-2|-1)(m>0),
∵f(x)的图象为偶函数,图象关于y轴对称,图象如下图所示,
令f(x)=0可得x=1,3,-1,-3
∴y=f[f(x)]=0时可得,f(x)=1或f(x)=3或f(x)=-1,或f(x)=-3
①当m>3时,结合函数的图象可知,y=f[f(x)]有16个零点;
②m=3时,结合函数的图象可知,y=f[f(x)]有13个零点;
③1<m<3时,结合函数的图象可知,y=f[f(x)]有8个零点;
④m=1时,结合函数的图象可知,y=f[f(x)]有7个零点;
⑤0<m<1时,结合函数的图象可知,y=f[f(x)]有4个零点;
故选A
点评 本题主要考查了函数的零点的求解,解题的关键是数形结合思想的应用.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
6.如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=2,A1A=2,则直线BC1到平面D1AC的距离为( )


| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{2}{3}$ | D. | $\frac{4}{3}$ |
7.经过椭圆x2+2y2=2的一个焦点作倾斜角为45°的直线l,交椭圆于M,N两点,设O为坐标原点,则$\overrightarrow{OM}$•$\overrightarrow{ON}$等于( )
| A. | -3 | B. | ±$\frac{1}{3}$ | C. | -$\frac{1}{3}$ | D. | -$\frac{1}{2}$ |
 如图$\overrightarrow{OA}$,$\overrightarrow{OB}$不共线,P点在AB上,求证:存在实数λ,μ且λ+μ=1,使$\overrightarrow{OP}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$.思考:有本题你想到了什么?(用向量证明三点共线)
如图$\overrightarrow{OA}$,$\overrightarrow{OB}$不共线,P点在AB上,求证:存在实数λ,μ且λ+μ=1,使$\overrightarrow{OP}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$.思考:有本题你想到了什么?(用向量证明三点共线)