题目内容
椭圆 =1的焦点为F1、F2,点P为椭圆上的动点,当∠F1PF2为钝角时,求点P的横坐标x0的取值范围.
=1的焦点为F1、F2,点P为椭圆上的动点,当∠F1PF2为钝角时,求点P的横坐标x0的取值范围.
 =1的焦点为F1、F2,点P为椭圆上的动点,当∠F1PF2为钝角时,求点P的横坐标x0的取值范围.
=1的焦点为F1、F2,点P为椭圆上的动点,当∠F1PF2为钝角时,求点P的横坐标x0的取值范围.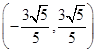
由题意F1(-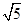 ,0),F2(
,0),F2(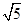 ,0),设P(x0,y0),则
,0),设P(x0,y0),则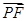 1=(-
1=(-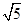 -x0,-y0),
-x0,-y0),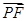 2=(
2=(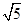 -x0,-y0),∴
-x0,-y0),∴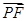 1·
1·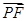 2=
2=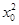 -5+
-5+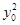 <0.①
<0.①
又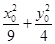 =1,② 由①②得
=1,② 由①②得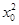 <
<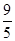 ,
,
∴-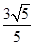 <x0<
<x0<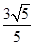 .则点P的横坐标x0的取值范围为
.则点P的横坐标x0的取值范围为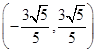 .
.
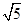 ,0),F2(
,0),F2(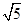 ,0),设P(x0,y0),则
,0),设P(x0,y0),则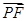 1=(-
1=(-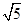 -x0,-y0),
-x0,-y0),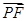 2=(
2=(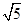 -x0,-y0),∴
-x0,-y0),∴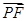 1·
1·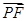 2=
2=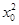 -5+
-5+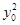 <0.①
<0.①又
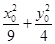 =1,② 由①②得
=1,② 由①②得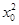 <
<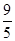 ,
,∴-
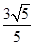 <x0<
<x0<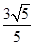 .则点P的横坐标x0的取值范围为
.则点P的横坐标x0的取值范围为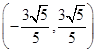 .
.
练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
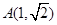 是离心率为
是离心率为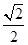 的椭圆
的椭圆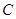 :
: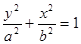
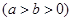 上的一点,斜率为
上的一点,斜率为 的直线
的直线 交椭圆
交椭圆 ,
, 两点,且
两点,且 、
、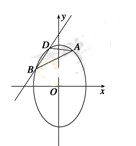
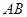 ,
,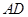 的斜率之和为定值.
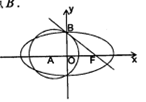
的斜率之和为定值. 为椭圆
为椭圆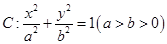 右焦点,圆
右焦点,圆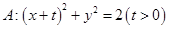 与椭圆
与椭圆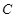 的一个公共点为
的一个公共点为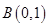 ,且直线
,且直线 与圆
与圆 相切与点
相切与点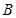 。
。
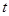 的值及椭圆
的值及椭圆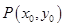 满足
满足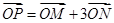 ,其中
,其中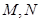 是椭圆
是椭圆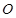 为原点,直线
为原点,直线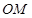 与
与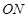 的斜率之积为
的斜率之积为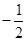 ,求证:
,求证: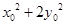 为定值。
为定值。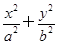 =1(a>b>0)的左、右焦点,点M在x轴上,且
=1(a>b>0)的左、右焦点,点M在x轴上,且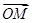 =
=
 ,过点F2的直线与椭圆交于A、B两点,且AM⊥x轴,
,过点F2的直线与椭圆交于A、B两点,且AM⊥x轴,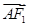 ·
·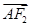 =0.
=0.
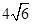 ,求椭圆的方程.
,求椭圆的方程.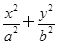 =1(a>b>0)的左、右焦点,A、B分别是此椭圆的右顶点和上顶点,P是椭圆上一点,O是坐标原点,OP∥AB,PF1⊥x轴,F1A=
=1(a>b>0)的左、右焦点,A、B分别是此椭圆的右顶点和上顶点,P是椭圆上一点,O是坐标原点,OP∥AB,PF1⊥x轴,F1A=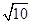 +
+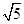 ,则此椭圆的方程是________________.
,则此椭圆的方程是________________.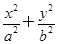 =1(a>b>0)的焦距为2c,以O为圆心,a为半径的圆.过点
=1(a>b>0)的焦距为2c,以O为圆心,a为半径的圆.过点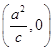 作圆的两切线互相垂直,则离心率e=________.
作圆的两切线互相垂直,则离心率e=________.
 的右准线方程是 .
的右准线方程是 .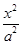 +
+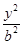 =1(a>b>0)的一个顶点为A(2,0),离心率为
=1(a>b>0)的一个顶点为A(2,0),离心率为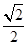 .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N. 时,求k的值.
时,求k的值.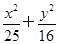 上的点.若F1、F2是椭圆的两个焦点,则|PF1|+|PF2|=________.
上的点.若F1、F2是椭圆的两个焦点,则|PF1|+|PF2|=________.