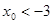题目内容
(1)若抛物线过直线 与圆
与圆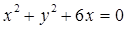 的交点, 且顶点在原点,坐标轴为对称轴,求抛物线的方程.
的交点, 且顶点在原点,坐标轴为对称轴,求抛物线的方程.
(2)已知双曲线与椭圆 共焦点,它们的离心率之和为
共焦点,它们的离心率之和为 ,求双曲线方程.
,求双曲线方程.
 与圆
与圆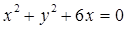 的交点, 且顶点在原点,坐标轴为对称轴,求抛物线的方程.
的交点, 且顶点在原点,坐标轴为对称轴,求抛物线的方程. (2)已知双曲线与椭圆
 共焦点,它们的离心率之和为
共焦点,它们的离心率之和为 ,求双曲线方程.
,求双曲线方程.(1) 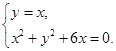 解得交点坐标为(0,0),(-3,-3).
解得交点坐标为(0,0),(-3,-3).
∵ (-3,-3) 在第三象限. 设方程为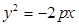 ,或
,或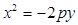 .
.
代入(-3,-3), 解得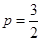 .∴ 所求的抛物线方程为
.∴ 所求的抛物线方程为 , 或
, 或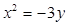 .
.
(2)椭圆 中
中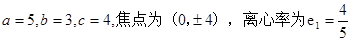 ,所以双曲线的离心率为
,所以双曲线的离心率为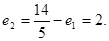 由双曲线的焦点为
由双曲线的焦点为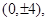 所以
所以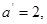 所以
所以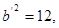 所以双曲线的方程为
所以双曲线的方程为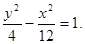
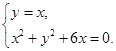 解得交点坐标为(0,0),(-3,-3).
解得交点坐标为(0,0),(-3,-3).∵ (-3,-3) 在第三象限. 设方程为
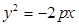 ,或
,或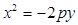 .
. 代入(-3,-3), 解得
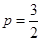 .∴ 所求的抛物线方程为
.∴ 所求的抛物线方程为 , 或
, 或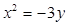 .
.(2)椭圆
 中
中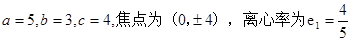 ,所以双曲线的离心率为
,所以双曲线的离心率为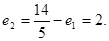 由双曲线的焦点为
由双曲线的焦点为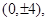 所以
所以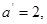 所以
所以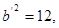 所以双曲线的方程为
所以双曲线的方程为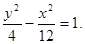
略

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 的焦点为
的焦点为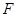 ,动点
,动点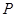 在直线
在直线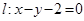 上
上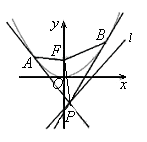
 为抛物线
为抛物线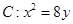 上一点,
上一点,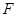 为抛物线
为抛物线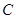 的焦点,以
的焦点,以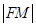 为半径的圆和抛物线的准线相交,则
为半径的圆和抛物线的准线相交,则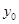 的取值范围是( )
的取值范围是( )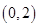
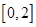
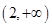
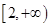
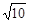 时, 求k的值.
时, 求k的值.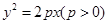 有一内接直角三角形,直角的顶点在原点,一直角边的方程是
有一内接直角三角形,直角的顶点在原点,一直角边的方程是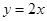 ,斜边长是
,斜边长是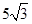 ,求此抛物线的方程。
,求此抛物线的方程。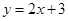 与抛物线
与抛物线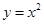 所围成的图形面积是_________________
所围成的图形面积是_________________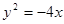 的焦点为F,其准线与x轴交于点M,过点M作斜率为k的直线l交抛物线于A、B两点,.
的焦点为F,其准线与x轴交于点M,过点M作斜率为k的直线l交抛物线于A、B两点,.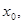 O),求证:
O),求证: