题目内容
要建造一座跨度为16米，拱高为4米的抛物线拱桥，建桥时每隔4米用一根支柱支撑，两边的柱长应为 ．
3米.
以抛物线的顶点为原点，对称轴为y轴建立直角坐标系，设抛物线的方程为
,因为A(8,-4)在抛物线上，得
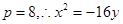,将x=4代入方程可得y="-1," 故两边的柱长应为4-1=3米.
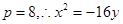,因为A(8,-4)在抛物线上，得,将x=4代入方程可得y="-1," 故两边的柱长应为4-1=3米.
练习册系列答案
相关题目
题目内容
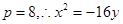,因为A(8,-4)在抛物线上，得,将x=4代入方程可得y="-1," 故两边的柱长应为4-1=3米.
上任意一点到点
的距离与到直线
的距离相等．
交曲线
、
两点，是否存在实数
，使得以
为直径的圆经过原点
？若存在，求出
的焦点为
，准线为
,
为抛物线上一点,
,
为垂足．如果直线
的斜率为
,那么
（
）的焦点为
，
为坐标原点，
为抛物线上一点，且
,
的面积为
，则该抛物线的方程为 .
是抛物线
上一个动点，则点
的距离与点
的距离和的最小值是 。
与圆
的交点， 且顶点在原点，坐标轴为对称轴，求抛物线的方程. 
共焦点，它们的离心率之和为
，求双曲线方程.
的焦点为F，点A、B、C在此抛物线上，点A坐标为(1, 2).若点F恰为
的重心，则直线BC的方程为
的焦点坐标是______________．
的焦点F的直线AB交抛物线于A，B两点，弦ＡＢ的中点为Ｍ，过Ｍ作ＡＢ的垂直平分线交ｘ轴于Ｎ，