题目内容
已知函数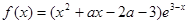 在
在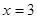 取得极值
取得极值
(1)求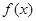 的单调区间(用
的单调区间(用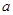 表示);
表示);
(2)设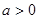 ,
,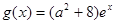 ,若存在
,若存在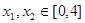 ,使得
,使得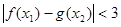 成立,求
成立,求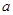 的取值范围.
的取值范围.
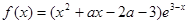 在
在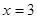 取得极值
取得极值(1)求
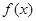 的单调区间(用
的单调区间(用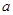 表示);
表示);(2)设
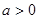 ,
,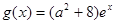 ,若存在
,若存在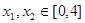 ,使得
,使得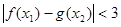 成立,求
成立,求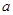 的取值范围.
的取值范围.(1) 见解析 (2) 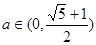
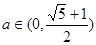
第一问利用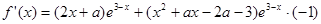
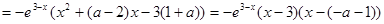
根据题意 在
在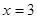 取得极值,
取得极值, 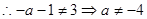
对参数a分情况讨论,可知
当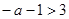 即
即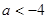 时递增区间:
时递增区间: 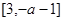 递减区间:
递减区间: 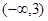 ,
, 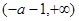
当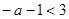 即
即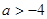 时递增区间:
时递增区间: 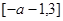 递减区间:
递减区间: 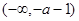 ,
, 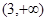
第二问中,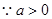 由(1)知:
由(1)知: 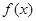 在
在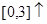 ,
, 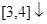
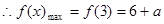 ,
,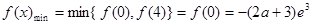
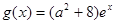 在
在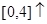
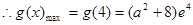
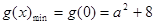
从而求解。
解: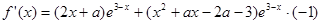
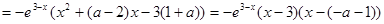 …..3分
…..3分
 在
在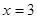 取得极值,
取得极值, 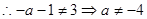 ……………………..4分
……………………..4分
(1) 当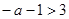 即
即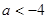 时 递增区间:
时 递增区间: 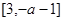 递减区间:
递减区间: 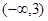 ,
, 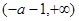
当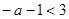 即
即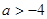 时递增区间:
时递增区间: 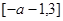 递减区间:
递减区间: 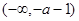 ,
, 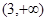 ………….6分
………….6分
(2)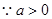 由(1)知:
由(1)知: 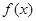 在
在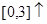 ,
, 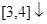
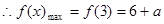 ,
,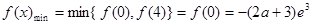
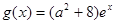 在
在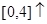
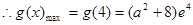
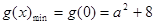 ……………….10分
……………….10分
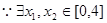 , 使
, 使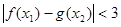 成立
成立
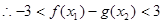
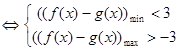
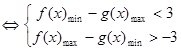
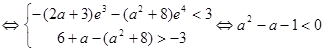 得:
得: 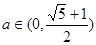
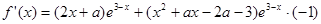
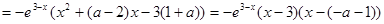
根据题意
 在
在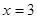 取得极值,
取得极值, 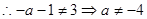
对参数a分情况讨论,可知
当
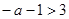 即
即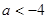 时递增区间:
时递增区间: 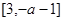 递减区间:
递减区间: 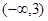 ,
, 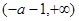
当
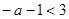 即
即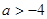 时递增区间:
时递增区间: 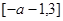 递减区间:
递减区间: 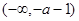 ,
, 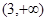
第二问中,
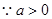 由(1)知:
由(1)知: 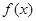 在
在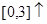 ,
, 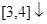
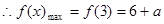 ,
,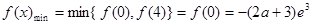
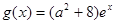 在
在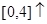
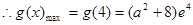
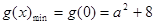
从而求解。
解:
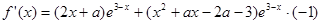
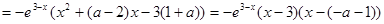 …..3分
…..3分 在
在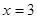 取得极值,
取得极值, 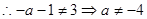 ……………………..4分
……………………..4分(1) 当
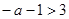 即
即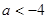 时 递增区间:
时 递增区间: 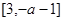 递减区间:
递减区间: 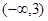 ,
, 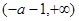
当
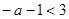 即
即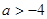 时递增区间:
时递增区间: 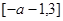 递减区间:
递减区间: 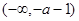 ,
, 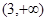 ………….6分
………….6分(2)
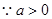 由(1)知:
由(1)知: 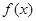 在
在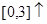 ,
, 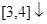
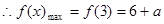 ,
,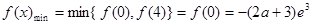
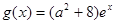 在
在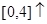
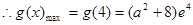
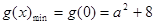 ……………….10分
……………….10分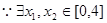 , 使
, 使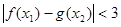 成立
成立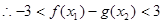
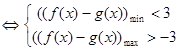
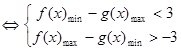
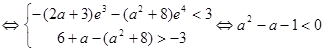 得:
得: 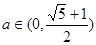

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,其中
,其中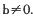
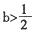 时,判断函数
时,判断函数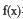 在定义域上的单调性;
在定义域上的单调性;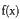 的极值点;
的极值点;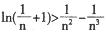 都成立.
都成立.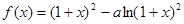 在
在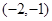 上是增函数,在
上是增函数,在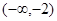 上为减函数.
上为减函数.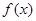 的表达式;
的表达式;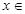
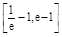 时,不等式
时,不等式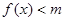 恒成立,求实数
恒成立,求实数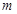 的值;
的值;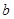 使得关于
使得关于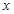 的方程
的方程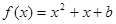 在区间[0,2]上恰好有两个相异的实根,若存在,求实数
在区间[0,2]上恰好有两个相异的实根,若存在,求实数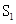 为直线
为直线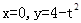 (
(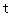 为常数)及
为常数)及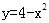 所围成的图形的面积,
所围成的图形的面积,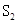 为直线
为直线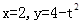 (
(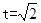 时,求
时,求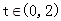 ,求
,求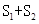 的最小值。
的最小值。
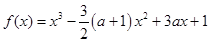 .
.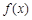 在区间
在区间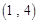 内单调递减,求
内单调递减,求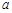 的取值范围;
的取值范围;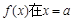 处取得极小值是
处取得极小值是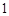 ,求
,求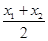 时,又称AB存在“中值伴随切线”.试问:在函数f(x)的图像上是否存在不同两点A,B,使得AB存在“中值伴随切线”?若存在,求出A,B的坐标;若不存在,说明理由
时,又称AB存在“中值伴随切线”.试问:在函数f(x)的图像上是否存在不同两点A,B,使得AB存在“中值伴随切线”?若存在,求出A,B的坐标;若不存在,说明理由
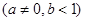 ,在区间
,在区间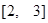 上有最大值4,最小值1,设函数
上有最大值4,最小值1,设函数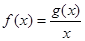 .
.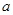 、
、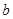 的值及函数
的值及函数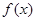 的解析式;
的解析式;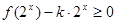 在
在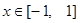 时恒成立,求实数
时恒成立,求实数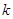 的取值范围;
的取值范围;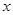 的方程
的方程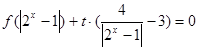 有三个相异的实数根,求实数
有三个相异的实数根,求实数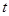 的取值范围.
的取值范围.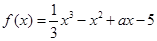 在区间
在区间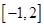 上不单调,则实数
上不单调,则实数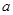 的取值范围是( ) .
的取值范围是( ) .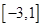
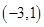
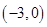
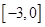
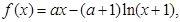 其中
其中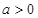 ,
,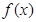 的单调区间;
的单调区间;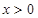 时,证明不等式:
时,证明不等式: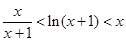 .
.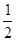 +
+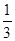 +
+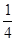 +L
+L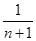 (
( ).
).