题目内容
如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的表面积(其中∠BAC=30°)及其体积.

旋转所得到的几何体的表面积为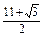
 R2 体积是
R2 体积是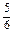
 R3
R3
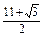
 R2 体积是
R2 体积是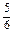
 R3
R3 如图所示,过C作CO1⊥AB于O1,
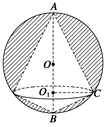
在半圆中可得∠BCA=90°,∠BAC=30°,AB=2R,
∴AC=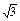 R,BC=R,CO1=
R,BC=R,CO1=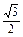 R,
R,
∴S球=4 R2,
R2,
 =
= ×
×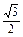 R×
R×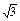 R=
R=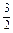
 R2,
R2,
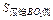 =
= ×
×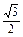 R×R=
R×R=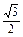
 R2,
R2,
∴S几何体表=S球+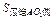 +
+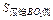
=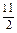
 R2+
R2+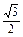
 R2=
R2=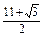
 R2,
R2,
∴旋转所得到的几何体的表面积为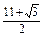
 R2.
R2.
又V球=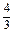
 R3,
R3,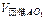 =
=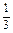 ·AO1·
·AO1· CO12=
CO12=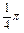 R2·AO1
R2·AO1
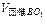 =
=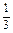 BO1·
BO1· CO12=
CO12=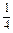 BO1·
BO1· R2
R2
∴V几何体=V球-(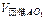 +
+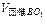 )
)
=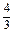
 R3-
R3-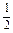
 R3=
R3=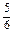
 R3.
R3.

在半圆中可得∠BCA=90°,∠BAC=30°,AB=2R,
∴AC=
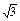 R,BC=R,CO1=
R,BC=R,CO1=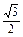 R,
R,∴S球=4
 R2,
R2,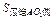 =
= ×
×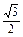 R×
R×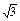 R=
R=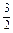
 R2,
R2,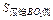 =
= ×
×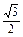 R×R=
R×R=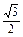
 R2,
R2,∴S几何体表=S球+
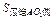 +
+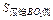
=
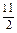
 R2+
R2+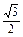
 R2=
R2=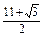
 R2,
R2,∴旋转所得到的几何体的表面积为
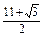
 R2.
R2.又V球=
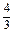
 R3,
R3,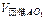 =
=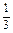 ·AO1·
·AO1· CO12=
CO12=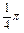 R2·AO1
R2·AO1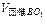 =
=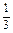 BO1·
BO1· CO12=
CO12=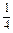 BO1·
BO1· R2
R2∴V几何体=V球-(
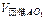 +
+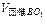 )
)=
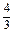
 R3-
R3-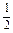
 R3=
R3=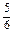
 R3.
R3.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的正方体
的正方体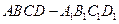 中,
中,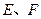 分别是
分别是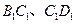 的中点,
的中点,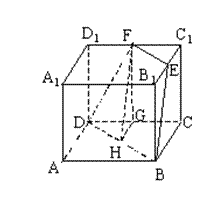
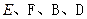 四点共面;
四点共面;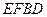 的面积.
的面积.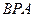 =
=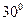 ,
,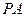 =
=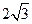 ,
,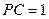 ,求圆
,求圆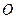 的半径。
的半径。
 的多面体的每一个面都外切于半径为
的多面体的每一个面都外切于半径为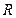 的一个球,求这个多面体的体积.
的一个球,求这个多面体的体积.



 倍 B.
倍 B.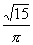 倍 C.
倍 C.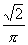 倍 D.
倍 D.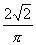 倍
倍