题目内容
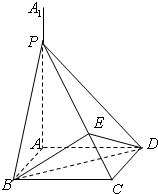 已知四边形ABCD是边长为1的正方形,且A1A⊥平面ABCD,P为A1A上一动点,过BD且垂直于PC的平面交PC于E,那么异面直线PC与BD所成的角的度数为
已知四边形ABCD是边长为1的正方形,且A1A⊥平面ABCD,P为A1A上一动点,过BD且垂直于PC的平面交PC于E,那么异面直线PC与BD所成的角的度数为分析:利用线面垂直的性质可得线线垂直;利用三角函数构造EH关于AP=x的函数,利用基本不等式求函数的最大值及取得最大值时的x值.
解答:解:连接BE,DE,∵平面BDE⊥PC,BD?平面BDE,
∴PC⊥BD,故异面直线PC与BD所成的角为90°;
连接AC,交BD于O,连接OE,过E作EH⊥AC,垂足为H,
∵A1A⊥平面ABCD,BD?平面ABCD,∴AA1⊥BD,又BD⊥AC,
∴BD⊥平面PAC,EH?平面PAC,∴EH⊥BD,BD∩AC=0,
∴EH⊥平面ABCD,又OE⊥PC,
在Rt△PAC中,PC=
,OC=
,
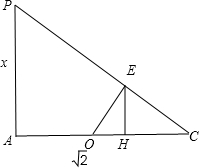
设PA=x,如图:
EH=
×cos∠C×sin∠C=
×
×
=
=
≤
=
VE-BCD=
×
×1×1×EH≤
×
=
,
当x=
时取“=”.
故答案是90°,
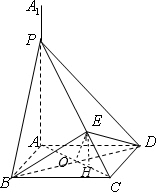
∴PC⊥BD,故异面直线PC与BD所成的角为90°;
连接AC,交BD于O,连接OE,过E作EH⊥AC,垂足为H,
∵A1A⊥平面ABCD,BD?平面ABCD,∴AA1⊥BD,又BD⊥AC,
∴BD⊥平面PAC,EH?平面PAC,∴EH⊥BD,BD∩AC=0,
∴EH⊥平面ABCD,又OE⊥PC,
在Rt△PAC中,PC=
| 2+x2 |
| ||
| 2 |
设PA=x,如图:
EH=
| ||
| 2 |
| ||
| 2 |
| ||
|
| x | ||
|
| x |
| 2+x2 |
| 1 | ||
|
| 1 | ||
2
|
| ||
| 4 |
VE-BCD=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| ||
| 4 |
| ||
| 24 |
当x=
| 2 |
故答案是90°,
| 2 |


点评:本题考查了线线垂直关系的判定,棱锥的体积计算,解答本题关键是利用三角函数构造EH关于AP=x的函数,体现了转化思想.

练习册系列答案
相关题目
 17、如图,已知四边形ABCD 是矩形,PA⊥平面ABCD,M,N分别是AB,PC的中点.
17、如图,已知四边形ABCD 是矩形,PA⊥平面ABCD,M,N分别是AB,PC的中点. 某城市计划在如图所示的空地ABCD上竖一块长方形液晶广告屏幕MNEF,宣传该城市未来十年计划、目标等相关政策.已知四边形ABCD是边长为30m的正方形,电源在点P处,点P到边AD、AB的距离分别为9m,3m,且MN~NE=16~9,线段MN必过点P,端点M、N分别在边AD、AB上,设AN=xm,液晶广告屏幕MNEF的面积为Sm2.
某城市计划在如图所示的空地ABCD上竖一块长方形液晶广告屏幕MNEF,宣传该城市未来十年计划、目标等相关政策.已知四边形ABCD是边长为30m的正方形,电源在点P处,点P到边AD、AB的距离分别为9m,3m,且MN~NE=16~9,线段MN必过点P,端点M、N分别在边AD、AB上,设AN=xm,液晶广告屏幕MNEF的面积为Sm2. 如图,已知四边形ABCD是菱形,PA⊥平面ABCD,PA=AB=BD=2,AC与BD交于E点,F是PD的中点.
如图,已知四边形ABCD是菱形,PA⊥平面ABCD,PA=AB=BD=2,AC与BD交于E点,F是PD的中点.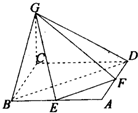 如图:已知四边形ABCD是边长为4的正方形,E、F分别是AB,AD的中点,GC垂直于ABCD所在平面,且GC=2.
如图:已知四边形ABCD是边长为4的正方形,E、F分别是AB,AD的中点,GC垂直于ABCD所在平面,且GC=2. 已知四边形ABCD是空间四边形,E,F,G,H分别是边AB,BC,CD,DA的中点,求证:四边形EFGH是平行四边形.
已知四边形ABCD是空间四边形,E,F,G,H分别是边AB,BC,CD,DA的中点,求证:四边形EFGH是平行四边形.