题目内容
 如图,已知四边形ABCD是菱形,PA⊥平面ABCD,PA=AB=BD=2,AC与BD交于E点,F是PD的中点.
如图,已知四边形ABCD是菱形,PA⊥平面ABCD,PA=AB=BD=2,AC与BD交于E点,F是PD的中点.(1)求证:PB∥平面AFC;
(2)求多面体PABCF的体积.
分析:(Ⅰ)连接EF,利用三角形中位线定理,结合线面平行的判定定理,不难证出PB∥平面AFC.
(II)由等边三角形面积公式,算出菱形ABCD长,从而得到四棱锥P-ABCD的体积.取AD的中点G,连接GF,可证出FG长为1且是三棱锥F-ACD的高,从而算出三棱锥F-ACD的体积,最后用两个体积相减,即得多面体PABCF的体积.
(II)由等边三角形面积公式,算出菱形ABCD长,从而得到四棱锥P-ABCD的体积.取AD的中点G,连接GF,可证出FG长为1且是三棱锥F-ACD的高,从而算出三棱锥F-ACD的体积,最后用两个体积相减,即得多面体PABCF的体积.
解答:解:(Ⅰ)连接EF,
∵四边形ABCD是菱形,∴对角线交点E为BD的中点,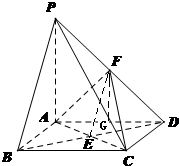
又∵F为PD的中点,∴PB∥EF
∵PB?平面AFC,EF⊆平面AFC,∴PB∥平面AFC.…(6分)
(Ⅱ)∵PA=AB=2,ABCD是菱形,∴△ABD为等边三角形
∴四边形ABCD的面积S=2S△ABD=2×
×22=2
,S△ACD=S△ABD=
,
取AD的中点G,连接GF,
∵FG为△PAD的中位线,∴FG∥PA且FG=
PA=1
∵PA⊥平面ABCD,∴FG⊥平面ABCD,
∴VP-ABCF=VP-ABCD-VF-ACD
×2
×2-
×
×1=
. …(12分)
∵四边形ABCD是菱形,∴对角线交点E为BD的中点,

又∵F为PD的中点,∴PB∥EF
∵PB?平面AFC,EF⊆平面AFC,∴PB∥平面AFC.…(6分)
(Ⅱ)∵PA=AB=2,ABCD是菱形,∴△ABD为等边三角形
∴四边形ABCD的面积S=2S△ABD=2×
| ||
| 4 |
| 3 |
| 3 |
取AD的中点G,连接GF,
∵FG为△PAD的中位线,∴FG∥PA且FG=
| 1 |
| 2 |
∵PA⊥平面ABCD,∴FG⊥平面ABCD,
∴VP-ABCF=VP-ABCD-VF-ACD
| 1 |
| 3 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
点评:本题考查空间中直线与直线、直线与平面的位置关系,空间直线平行的证明,多面体体积的计算等知识,考查空间想象能力、推理论证能力和运算求解能力,属于中等题.

练习册系列答案
相关题目
 如图,已知四边形ABCD为直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,沿AC将△ABC折起,使点B到点P的位置,且平面PAC⊥平面ACD.
如图,已知四边形ABCD为直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,沿AC将△ABC折起,使点B到点P的位置,且平面PAC⊥平面ACD. (几何证明选讲选做题)如图,已知四边形ABCD内接于⊙O,且AB为⊙O的直径,直线MN切
(几何证明选讲选做题)如图,已知四边形ABCD内接于⊙O,且AB为⊙O的直径,直线MN切 如图:已知四边形ABCD是正方形,PD⊥平面ABCD,PD=AD,点E,F分别是线段PB,AD的中点
如图:已知四边形ABCD是正方形,PD⊥平面ABCD,PD=AD,点E,F分别是线段PB,AD的中点 如图,已知四边形ABCD为直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,沿AC将△ABC折起,使点B到点P的位置,且平面PAC⊥平面ACD.
如图,已知四边形ABCD为直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,沿AC将△ABC折起,使点B到点P的位置,且平面PAC⊥平面ACD.