题目内容
 某城市计划在如图所示的空地ABCD上竖一块长方形液晶广告屏幕MNEF,宣传该城市未来十年计划、目标等相关政策.已知四边形ABCD是边长为30m的正方形,电源在点P处,点P到边AD、AB的距离分别为9m,3m,且MN~NE=16~9,线段MN必过点P,端点M、N分别在边AD、AB上,设AN=xm,液晶广告屏幕MNEF的面积为Sm2.
某城市计划在如图所示的空地ABCD上竖一块长方形液晶广告屏幕MNEF,宣传该城市未来十年计划、目标等相关政策.已知四边形ABCD是边长为30m的正方形,电源在点P处,点P到边AD、AB的距离分别为9m,3m,且MN~NE=16~9,线段MN必过点P,端点M、N分别在边AD、AB上,设AN=xm,液晶广告屏幕MNEF的面积为Sm2.(1)求S关于x的函数关系式及其定义域;
(2)若液晶屏每平米造价为1500元,当x为何值时,液晶广告屏幕MNEF的造价最低?
分析:(1)先确定AM、MN的长,进而可得S关于x的函数关系式及其定义域;
(2)要使液晶广告屏幕MNEF的造价最低,即使液晶广告屏幕MNEF的面积S最小,利用导数的方法,即可求得结论.
(2)要使液晶广告屏幕MNEF的造价最低,即使液晶广告屏幕MNEF的面积S最小,利用导数的方法,即可求得结论.
解答:解:(1)由题意,在△AMN中,
=
,
=
∴
+
=1,∴AM=
∴MN=
=
∵0≤AM≤30,0≤x≤30,,10≤x≤30
∴S=
[x2+
],其定义域为[10,30];
(2)由题意,要使液晶广告屏幕MNEF的造价最低,即使液晶广告屏幕MNEF的面积S最小
设f(x)=
[x2+
](x∈[10,30]),则f′(x)=
×
令f′(x)=0,的x=9+3
因为10≤x<9+3
时,f'(x)<0;9+3
<x≤30时,f'(x)>0,
所以x=9+3
时,S取得最小值,即液晶广告屏幕MNEF的造价最低.
故当x=9+3
时,液晶广告屏幕的造价最低.
| 9 |
| x |
| MP |
| MN |
| 3 |
| AM |
| NP |
| MN |
∴
| 9 |
| x |
| 3 |
| AM |
| 3x |
| x-9 |
∴MN=
| AM2+AN2 |
x2+
|
∵0≤AM≤30,0≤x≤30,,10≤x≤30
∴S=
| 9 |
| 16 |
| 9x2 |
| (x-9)2 |
(2)由题意,要使液晶广告屏幕MNEF的造价最低,即使液晶广告屏幕MNEF的面积S最小
设f(x)=
| 9 |
| 16 |
| 9x2 |
| (x-9)2 |
| 9 |
| 16 |
| 2x[(x-9)3-81] |
| (x-9)3 |
令f′(x)=0,的x=9+3
| 3 | 3 |
因为10≤x<9+3
| 3 | 3 |
| 3 | 3 |
所以x=9+3
| 3 | 3 |
故当x=9+3
| 3 | 3 |
点评:本题考查四边形面积的计算,考查导数知识,考查学生的计算能力,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 上竖一块长方形液晶广告屏幕
上竖一块长方形液晶广告屏幕 ,宣传该城市未来十年计划、目标等相关政策.已知四边形
,宣传该城市未来十年计划、目标等相关政策.已知四边形 处,点
处,点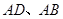 的距离分别为9米,3米,且
的距离分别为9米,3米,且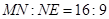 ,线段
,线段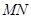 必过点
必过点 分别在边
分别在边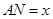 米,液晶广告屏幕
米,液晶广告屏幕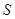 平方米.
平方米.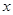 的函数关系式及其定义域;
的函数关系式及其定义域;
 某城市计划在如图所示的空地ABCD上竖一块长方形液晶广告屏幕MNEF,宣传该城市未来十年计划、目标等相关政策.已知四边形ABCD是边长为30m的正方形,电源在点P处,点P到边AD、AB的距离分别为9m,3m,且MN~NE=16~9,线段MN必过点P,端点M、N分别在边AD、AB上,设AN=xm,液晶广告屏幕MNEF的面积为Sm2.
某城市计划在如图所示的空地ABCD上竖一块长方形液晶广告屏幕MNEF,宣传该城市未来十年计划、目标等相关政策.已知四边形ABCD是边长为30m的正方形,电源在点P处,点P到边AD、AB的距离分别为9m,3m,且MN~NE=16~9,线段MN必过点P,端点M、N分别在边AD、AB上,设AN=xm,液晶广告屏幕MNEF的面积为Sm2.