Question

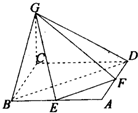如图：已知四边形ABCD是边长为4的正方形，E、F分别是AB，AD的中点，GC垂直于ABCD所在平面，且GC=2．
（1）求异面直线BC与GE所成的角的余弦值；
（2）求平面CBG与平面BGD的夹角的余弦值；
（3）求三棱锥D-GEF的体积．

Answer 1

分析：（1）以C为原点，CB为x轴，CD为y轴，CG为z轴建立空间直角坐标．用坐标表示向量，再利用夹角公式，可求异面直线BC与GE所成的角的余弦值；
（2）分别求出平面BCG、平面BDG的单位法向量，再利用夹角公式，求平面CBG与平面BGD的夹角的余弦值；
（3）根据GC⊥平面ABCD，可知GC为三棱锥G-DEF的高，利用V_D-GEF=V_G-DEF，可求三棱锥D-GEF的体积．

解答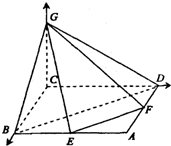：解：如图，以C为原点，CB为x轴，CD为y轴，CG为z轴建立空间直角坐标．
则依题意，有C（0，0，0），B（4，0，0），E（4，2，0），
F（2，4，0），D（0，4，0），G（0，0，2）．
（1）

CB

=（4，0，0），

GE

=（4，2，-2），
∴|

CB

|=4，|

GE

|=2

6

，
∴cos＜

CB

，

GE

＞=

16

8 6

=

6

3

…（4分）
（2）由题意可知，平面BCG的单位法向量

a

=（0，1，0），
设平面BDG的单位法向量为

b

=（x，y，z），
∵

BG

=（-4，0，2），

DG

=（0，-4，2），

b

⊥

BG

，

b

⊥

DG

得

x2+y2+z2=1 -4x+2z=0 -4y+2z=0

，∴

x= 6 6 y= 6 6 z= 6 3

，或

x=- 6 6 y=- 6 6 z=- 6 3

，
取

b

=(

6

6

，

6

6

，

6

3

)
∴cos＜

a

，

b

＞=

a • b

| a |•| b |

=(0，1，0)•(

6

6

，

6

6

，

6

3

)=

6

6

．…（8分）
（3）∵四边形ABCD是边长为4的正方形，E、F分别是AB、AD的中点，
∴EF∥BD且EF与BD间的距离为

1

4

|AC|=

2

，
又|EF|=

1

2

|BD|=2

2

∴S△DEF=

1

2

×2

2

×

2

=2．
又GC⊥平面ABCD，所以GC为三棱锥G-DEF的高，
∴VD-GEF=VG-DEF=

1

3

S△DEF|CG|=

4

3

．…（12分）

点评：本题以线面垂直为载体，考查空间向量的运用，考查线线角，面面角，考查三棱锥的体积，关键是构建空间直角坐标系．