题目内容
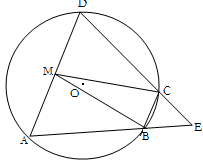
如图,四边形 是
是 的内接四边形,
的内接四边形,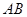 的延长线与
的延长线与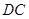 的延长线交于点
的延长线交于点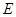 ,且
,且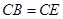 .
.
(I)证明: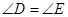 ;
;
(II)设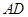 不是
不是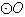 的直径,
的直径,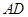 的中点为
的中点为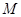 ,且
,且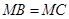 ,证明:
,证明: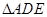 为等边三角形.
为等边三角形.
 是
是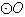 的内接四边形,
的内接四边形,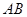 的延长线与
的延长线与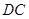 的延长线交于点
的延长线交于点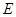 ,且
,且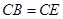 .
.
(I)证明:
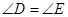 ;
;(II)设
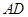 不是
不是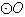 的直径,
的直径,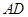 的中点为
的中点为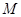 ,且
,且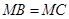 ,证明:
,证明: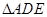 为等边三角形.
为等边三角形.(1)详见解析;(2)详见解析
试题分析:(1)根据题意可知A,B,C,D四点共圆,利用对角互补的四边形有外接圆这个结论可得:
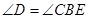 ,由已知得
,由已知得 ,故
,故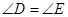 ;(2)不妨设出BC的中点为N,连结MN,则由
;(2)不妨设出BC的中点为N,连结MN,则由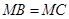 ,由等腰三角形三线合一可得:
,由等腰三角形三线合一可得: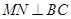 ,故O在直线MN上,又AD不是圆O的直径,M为AD的中点,故
,故O在直线MN上,又AD不是圆O的直径,M为AD的中点,故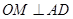 ,即
,即 ,所以
,所以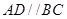 ,故
,故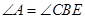 ,又
,又 ,故
,故 ,由(1)知,
,由(1)知,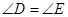 ,所以
,所以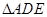 为等边三角形.
为等边三角形.试题解析:(1)由题设知A,B,C,D四点共圆,所以
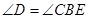 ,
,由已知得
 ,故
,故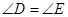 .
.(2)设BC的中点为N,连结MN,则由
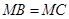 知
知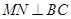 ,
,故O在直线MN上.
又AD不是圆O的直径,M为AD的中点,故
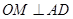 ,
,即
 .
.所以
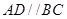 ,故
,故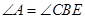 ,
,又
 ,故
,故 .
.由(1)知,
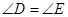 ,所以
,所以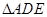 为等边三角形.
为等边三角形.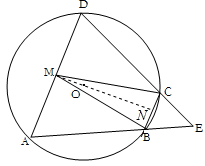

练习册系列答案
相关题目


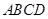 中,
中,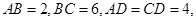 则四边形
则四边形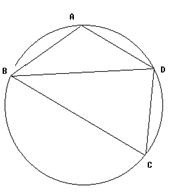
 是圆的内接三角形,
是圆的内接三角形, 的平分线交圆于点
的平分线交圆于点 ,交
,交 于点
于点 ,过点
,过点 的圆的切线与
的圆的切线与 的延长线交于点
的延长线交于点 .在上述条件下,给出下列四个结论:
.在上述条件下,给出下列四个结论:


 b
b b
b ,则线段CD的长为________.
,则线段CD的长为________.
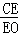 的值为 _________ .
的值为 _________ .