题目内容
如图所示,校园内计划修建一个矩形花坛并在花坛内装置两个相同的喷水器。已知喷水器的喷水区域是半径为5m的圆。问如何设计花坛的尺寸和两个喷水器的位置,才能使花坛的面积最大且能全部喷到水?
花坛的长为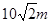 ,宽为
,宽为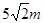 ,两喷水器位于矩形分成的两个正方形的中心.
,两喷水器位于矩形分成的两个正方形的中心.
解析试题分析:设花坛的长、宽分别为x m ,y m,根据要求,矩形花坛应在喷水区域内,顶点应恰好位于喷水区域的边界。依题意得: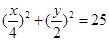 ,(
,(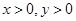 )
)
问题转化为在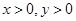 ,
,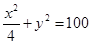 的条件下,求
的条件下,求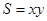 的最大值。
的最大值。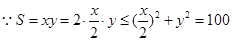 ,
,
由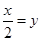 和
和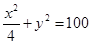 及
及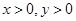 得:
得: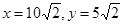
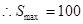
答:花坛的长为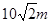 ,宽为
,宽为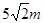 ,两喷水器位于矩形分成的两个正方形的中心,则符合要求。
,两喷水器位于矩形分成的两个正方形的中心,则符合要求。
考点:函数模型的选择与应用.
点评:本小题主要考查函数模型的选择与应用、基本不等式等,属于基础题.解决实际问题通常有四个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果;(4)转译成具体问题作出解答,其中关键是建立数学模型.

练习册系列答案
相关题目
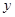 (万元)随投资收益
(万元)随投资收益 (万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%.
(万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%. 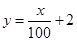 ;②
;②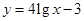 .
.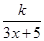 (0
(0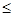 x
x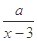 +10(x-6)2,(其中3<x<6,
+10(x-6)2,(其中3<x<6, 为常数,)已知销售价格为5元/千克时,每日可售出该商品11千克。
为常数,)已知销售价格为5元/千克时,每日可售出该商品11千克。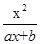 (a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.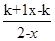 .
.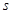 平方米,矩形一边的长为
平方米,矩形一边的长为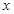 米(如图所示)
米(如图所示)
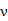 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度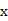 (单位:辆/千米)的函数。当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时。研究表明当
(单位:辆/千米)的函数。当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时。研究表明当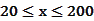 时,车流速度
时,车流速度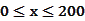 时,求函数
时,求函数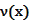 的表达式;
的表达式;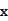 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)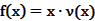 可以达到最大?并求出最大值。(精确到1辆/小时)
可以达到最大?并求出最大值。(精确到1辆/小时) 元(1≤a≤3)的管理费,预计当每件商品的售价为
元(1≤a≤3)的管理费,预计当每件商品的售价为 元(8≤x≤9)时,一年的销售量为(10-x)2万件.
元(8≤x≤9)时,一年的销售量为(10-x)2万件.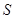 平方米.
平方米.
 表示
表示 和用
和用