题目内容
某连锁分店销售某种商品,每件商品的成本为4元,并且每件商品需向总店交 元(1≤a≤3)的管理费,预计当每件商品的售价为
元(1≤a≤3)的管理费,预计当每件商品的售价为 元(8≤x≤9)时,一年的销售量为(10-x)2万件.
元(8≤x≤9)时,一年的销售量为(10-x)2万件.
(1)求该连锁分店一年的利润L(万元)与每件商品的售价x的函数关系式L(x);
(2)当每件商品的售价为多少元时,该连锁分店一年的利润L最大,并求出L的最
大值M(a).
(1)L(x)= (x-4-a)(10-x)2,x∈[8,9] (2)最大值为16-4a
解析试题分析:(1)该连锁分店一年的利润L(万元)与售价x的函数关系式为
L(x)= (x-4-a)(10-x)2,x∈[8,9].
(2)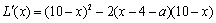 =(10-x)(18+2a-3x),
=(10-x)(18+2a-3x),
令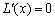 ,得x =6+
,得x =6+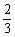 a或x=10(舍去).∵1≤a≤3,∴
a或x=10(舍去).∵1≤a≤3,∴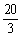 ≤6+
≤6+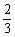 a≤8.
a≤8.
所以L(x)在x∈[8,9]上单调递减,故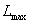 =L(8)=(8-4-a)(10-8)2=16-4a.
=L(8)=(8-4-a)(10-8)2=16-4a.
即M(a) =16-4a.
答:当每件商品的售价为8元时,该连锁分店一年的利润L最大,
最大值为16-4a万元.
考点:根据实际问题选择函数类型;利用导数求闭区间上函数的最值.
点评:考查学生根据实际问题选择函数类型的能力,以及利用导数求闭区间上函数最值的能力.

练习册系列答案
相关题目


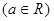
 在点
在点 处的切线与
处的切线与 轴和直线
轴和直线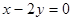 围成的三角形面积等于
围成的三角形面积等于 ,求
,求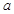 的值;
的值;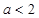 时,讨论
时,讨论 的单调性.
的单调性.
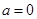 ,解不等式
,解不等式 ;
;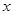 的不等式
的不等式
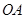 ,
,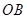 是某地一个湖泊的两条互相垂直的湖堤,线段
是某地一个湖泊的两条互相垂直的湖堤,线段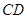 和曲线段
和曲线段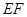 分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥
分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥 分别修建与
分别修建与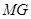 、
、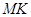 ,且以
,且以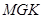 .建立如图2所示的直角坐标系,测得线段
.建立如图2所示的直角坐标系,测得线段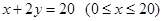 ,曲线段
,曲线段 ,设点
,设点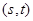 ,记
,记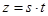 .(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度)
.(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度)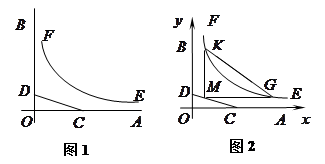
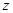 的取值范围;
的取值范围;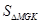 关于
关于 .
.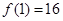 ,函数
,函数 是R上的奇函数,当
是R上的奇函数,当 时
时 ,
, 与
与 的值;
的值;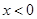 时,求
时,求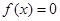 的两根中,一根属于区间
的两根中,一根属于区间 ,另一根属于区间
,另一根属于区间 ,求实数
,求实数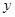 (升)关于行驶速度
(升)关于行驶速度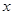 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: 已知甲、乙两地相距100千米.
已知甲、乙两地相距100千米.
 ,画出函数
,画出函数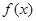 的图像,并求出函数
的图像,并求出函数 的零点;
的零点; ,且对任意
,且对任意 ,
,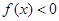 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.