题目内容
某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x (单位:元/千克)满足关系式y=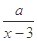 +10(x-6)2,(其中3<x<6,
+10(x-6)2,(其中3<x<6, 为常数,)已知销售价格为5元/千克时,每日可售出该商品11千克。
为常数,)已知销售价格为5元/千克时,每日可售出该商品11千克。
(I)求 的值;
的值;
(II)若该商品的成品为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大。
(I)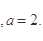 (II)当x=4时,函数
(II)当x=4时,函数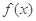 取得最大值,且最大值等于42。
取得最大值,且最大值等于42。
解析试题分析:(I)因为x=5时,y=11,所以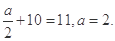 (4分)
(4分)
(II)由(I)可知,该商品每日的销售量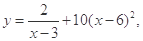
所以商场每日销售该商品所获得的利润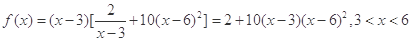
从而,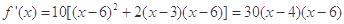 (8分)
(8分)
于是,当x变化时,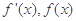 的变化情况如下表:
的变化情况如下表: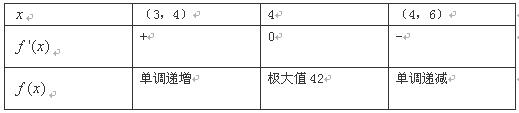
由上表可得,x=4是函数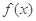 在区间(3,6)内的极大值点,也是最大值点; (11分)
在区间(3,6)内的极大值点,也是最大值点; (11分)
所以,当x=4时,函数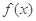 取得最大值,且最大值等于42。 (12)分
取得最大值,且最大值等于42。 (12)分
考点:函数模型,利用导数研究函数的最值,均值定理的应用。
点评:中档题,函数应用问题,在高考题中常常出现,一般的,需要“审清题意,设出变量,构建函数模型,解决数学问题”。求最值时 ,可利用均值定理,有时也可利用导数。应用均值定理,注意“一正,二定,三相等”,缺一不可。本题利用导数“表解法”,清晰明了。

练习册系列答案
相关题目
 对于任意的
对于任意的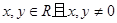 满足
满足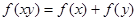 .
.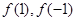 的值;
的值; 为偶函数;
为偶函数;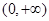 上是增函数,解不等式
上是增函数,解不等式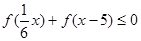
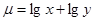 的最大值。
的最大值。 (如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为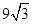 平方米,且高度不低于
平方米,且高度不低于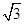 米,设防洪堤横断面的腰长为
米,设防洪堤横断面的腰长为 米,外周长(梯形的上底线段BC与两腰长的和)为
米,外周长(梯形的上底线段BC与两腰长的和)为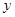 米.
米.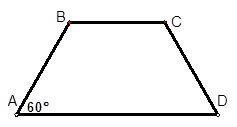


 在点
在点 处的切线与
处的切线与 轴和直线
轴和直线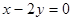 围成的三角形面积等于
围成的三角形面积等于 ,求
,求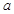 的值;
的值;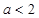 时,讨论
时,讨论 的单调性.
的单调性.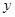 (升)关于行驶速度
(升)关于行驶速度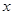 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: 已知甲、乙两地相距100千米.
已知甲、乙两地相距100千米.