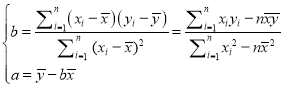题目内容
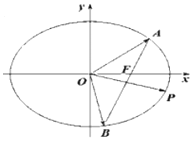
【题目】在平面直角坐标系![]() 中,已知椭圆C:
中,已知椭圆C:![]() (
(![]() >
>![]() >0)的右焦点为F(1,0),且过点(1,
>0)的右焦点为F(1,0),且过点(1,![]() ),过点F且不与
),过点F且不与![]() 轴重合的直线
轴重合的直线![]() 与椭圆C交于A,B两点,点P在椭圆上,且满足
与椭圆C交于A,B两点,点P在椭圆上,且满足![]() .
.
(1)求椭圆C的标准方程;
(2)若![]() ,求直线AB的方程.
,求直线AB的方程.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】
(1)![]() 代入椭圆方程,结合
代入椭圆方程,结合![]() 关系,即可求出椭圆标准方程;
关系,即可求出椭圆标准方程;
(2)设直线![]() 方程,与椭圆联立,利用韦达定理,得出
方程,与椭圆联立,利用韦达定理,得出![]() 两点的坐标关系,进而求出
两点的坐标关系,进而求出![]() 点坐标,代入椭圆方程,即可求出直线
点坐标,代入椭圆方程,即可求出直线![]() 方程.
方程.
(1)由题意可知,![]() =1,且
=1,且![]()
又因为![]() ,
,
解得![]() ,
,![]() ,
,
所以椭圆C的标准方程为![]() ;
;
(2)若直线AB的斜率不存在,则易得![]() ,
,![]() ,
,
∴![]() ,得P(
,得P(![]() ,0),
,0),
显然点P不在椭圆上,舍去;
因此设直线![]() 的方程为
的方程为![]() ,设
,设![]() ,
,![]() ,
,
将直线![]() 的方程与椭圆C的方程联立
的方程与椭圆C的方程联立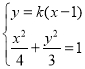 ,
,
整理得![]() ,
,
∴![]() ,
,
则由![]()
得![]()
將P点坐示代入椭圆C的方程,
得![]() (*);
(*);
将![]() 代入等式(*)得
代入等式(*)得![]()
∴![]()
因此所求直线AB的方程为![]() .
.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
【题目】某校从2011年到2018年参加“北约”,“华约”考试而获得加分的学生(每位学生只能参加“北约”,“华约”一种考试)人数可以通过以下表格反映出来.(为了方便计算,将2011年编号为1,2012年编号为2,依此类推……)
年份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
人数y | 2 | 3 | 4 | 4 | 7 | 7 | 6 | 6 |
(1)据悉,该校2018年获得加分的6位同学中,有1位获得加20分,2位获得加15分,3位获得加10分,从该6位同学中任取两位,记该两位同学获得的加分之和为X,求X的分布列及期望.
(2)根据最近五年的数据,利用最小二乘法求出y与x之间的线性回归方程,并用以预测该校2019年参加“北约”,“华约”考试而获得加分的学生人数.(结果要求四舍五入至个位)
参考公式: