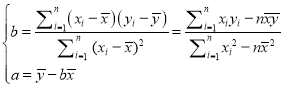题目内容
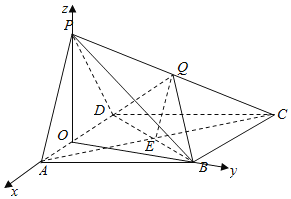
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() 为矩形,
为矩形,![]() ,
,![]() 均为等边三角形,
均为等边三角形,![]() ,
,![]() .
.
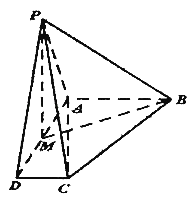
(Ⅰ)过![]() 作截面与线段
作截面与线段![]() 交于点
交于点![]() ,使得
,使得![]() 平面
平面![]() ,试确定点
,试确定点![]() 的位置,并予以证明;
的位置,并予以证明;
(Ⅱ)在(Ⅰ)的条件下,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)![]() 为线段
为线段![]() 的中点,证明见解析(Ⅱ)
的中点,证明见解析(Ⅱ)![]()
【解析】
(Ⅰ)取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,
,![]() ,且
,且![]() .可得
.可得![]() ,从而
,从而![]() 面
面![]() ,即面
,即面![]() 面
面![]() .
.
(Ⅱ)连结![]() 交
交![]() 于
于![]() ,则
,则![]() 为
为![]() 的中点,连结
的中点,连结![]() ,当
,当![]() 面
面![]() 时,
时,![]() ,所以
,所以![]() 是
是![]() 中点.由(1)知
中点.由(1)知![]() ,
,![]() ,
,![]() 两两垂直,分别以
两两垂直,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系,利用向量求解.
轴建立空间直角坐标系,利用向量求解.
解:(Ⅰ)取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,
,
![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() ,
,![]() ,
,
又![]() ,
,![]() ,且
,且![]() .
.
于是![]() ,从而
,从而![]() .
.
![]()
![]() 面
面![]() ,
,![]() 面
面![]() ,
,![]()
所以![]() 面
面![]() ,而
,而![]() 面
面![]() ,所以面
,所以面![]() 面
面![]() .
.
(Ⅱ)连结![]() 交
交![]() 于
于![]() ,则
,则![]() 为
为![]() 的中点,连结
的中点,连结![]() ,当
,当![]() 面
面![]() 时,
时,![]() ,所以
,所以![]() 是
是![]() 中点.
中点.
由(Ⅰ)知![]() ,
,![]() ,
,![]() 两两垂直,分别以
两两垂直,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则![]() ,
,![]() ,
, ![]() ,
, ![]() ,
,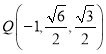 ,
,
![]() ,
,![]() .
.
设面![]() 的法向量为
的法向量为![]() ,由
,由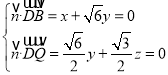 ,取
,取![]() .
.
面![]() 的法向量是
的法向量是![]() ,
,
![]()
![]() ,
,![]() ,
,![]()
![]() .
.
![]() 二面角
二面角![]() 是钝角,
是钝角,![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.

【题目】某医科大学实习小组为研究实习地昼夜温差与患感冒人数之间的关系,分别到当地气象部门和某医院抄录了1月份至3月份每月5日、20日的昼夜温差情况与因患感冒而就诊的人数,得到如表资料:
日期 | 1月5日 | 1月20日 | 2月5日 | 2月20日 | 3月5日 | 3月20日 |
昼夜温差 | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数 | 22 | 25 | 29 | 26 | 16 | 12 |
该小组确定的研究方案是:先从这六组数据中随机选取4组数据求线性回归方程,再用剩余的2组数据进行检验.
(1)求剩余的2组数据都是20日的概率;
(2)若选取的是1月20日,2月5日,2月20日,3月5日四组数据.
①请根据这四组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (
(![]() ,
,![]() 用分数表示);
用分数表示);
②若某日的昼夜温差为![]() ,预测当日就诊人数约为多少人?
,预测当日就诊人数约为多少人?
附参考公式: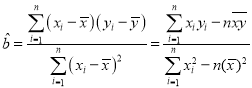 ,
,![]() .
.
【题目】某校从2011年到2018年参加“北约”,“华约”考试而获得加分的学生(每位学生只能参加“北约”,“华约”一种考试)人数可以通过以下表格反映出来.(为了方便计算,将2011年编号为1,2012年编号为2,依此类推……)
年份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
人数y | 2 | 3 | 4 | 4 | 7 | 7 | 6 | 6 |
(1)据悉,该校2018年获得加分的6位同学中,有1位获得加20分,2位获得加15分,3位获得加10分,从该6位同学中任取两位,记该两位同学获得的加分之和为X,求X的分布列及期望.
(2)根据最近五年的数据,利用最小二乘法求出y与x之间的线性回归方程,并用以预测该校2019年参加“北约”,“华约”考试而获得加分的学生人数.(结果要求四舍五入至个位)
参考公式: