题目内容
5.设随机变量X~B(2,P),随机变量Y~B(3,P),若P(X≥1)=$\frac{5}{9}$,则D(3Y+1)=( )| A. | 2 | B. | 3 | C. | 6 | D. | 7 |
分析 由X~B(2,P)和P(X≥1)的概率的值,可得到关于P的方程,解出P的值,再由方差公式可得到结果.
解答 解:∵随机变量X~B(2,P),
∴P(X≥1)=1-P(X=0)=1-${C}_{2}^{0}$(1-P)2=$\frac{5}{9}$,
解得P=$\frac{1}{3}$.
∴D(Y)=3×$\frac{1}{3}$×$\frac{2}{3}$=$\frac{2}{3}$,
∴D(3Y+1)=9×$\frac{2}{3}$=6,
故选:C.
点评 本题考查二项分布与n次独立重复试验的,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.下列函数是奇函数的是( )
| A. | f(x)=x|x| | B. | f(x)=lgx | C. | f(x)=2x+2-x | D. | f(x)=x3-1 |
13.若复数z满足1-z=z•i,则z等于( )
| A. | -$\frac{1}{2}$-$\frac{1}{2}$i | B. | -$\frac{1}{2}$+$\frac{1}{2}$i | C. | $\frac{1}{2}$-$\frac{1}{2}$i | D. | $\frac{1}{2}$+$\frac{1}{2}$i |
10.某高校“统计初步”课程教师随机调查了选该课的一些学生情况,共调查了50人,其中女生27人,男生23人,女生中有20人选统计专业,另外7人选非统计专业;男生中有10人选统计专业,另外13人选非统计专业.
(Ⅰ)根据以上数据完成下列2×2列联表:
(Ⅱ)根据以上数据,能否在犯错误的概率不超过0.05的前提下,认为主修统计专业与性别有关系?
参考数据:附:X2=$\frac{n(ad-bc)^{2}}{(a+c)(b+d)(a+b)(c+d)}$
当X2≤2.706时,没有充分的证据判定变量A,B有关联,可以认为变量A,B是没有关联的;
当X2>2.706时,有90%的把握判定变量A,B有关联;
当X2>3.814时,有95%的把握判定变量A,B有关联;
当X2>6.635时,有99%的把握判定变量A,B有关联.
(Ⅰ)根据以上数据完成下列2×2列联表:
| 专业 性别 | 非统计专业 | 统计专业 | 总计 |
| 男 | |||
| 女 | |||
| 总计 |
参考数据:附:X2=$\frac{n(ad-bc)^{2}}{(a+c)(b+d)(a+b)(c+d)}$
当X2≤2.706时,没有充分的证据判定变量A,B有关联,可以认为变量A,B是没有关联的;
当X2>2.706时,有90%的把握判定变量A,B有关联;
当X2>3.814时,有95%的把握判定变量A,B有关联;
当X2>6.635时,有99%的把握判定变量A,B有关联.
17.从1,2,3,4这四个数中一次随机选取两个数,所取两个数之和为5的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
14.下列各函数中,最小值为2的是( )
| A. | y=x+$\frac{1}{x}$ | B. | y=sinx+$\frac{1}{sinx}$,x∈(0,$\frac{π}{2}$) | ||
| C. | y=$\frac{{{x^2}+3}}{{\sqrt{{x^2}+2}}}$ | D. | y=5x+5-x |
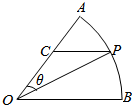 如图,扇形AOB,圆心角AOB等于60°,半径为2,在弧AB上有一动点P,过P引平行于OB的直线和OA交于点C,设∠AOP=θ.
如图,扇形AOB,圆心角AOB等于60°,半径为2,在弧AB上有一动点P,过P引平行于OB的直线和OA交于点C,设∠AOP=θ.