题目内容
已知函数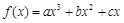 (
( )是定义在
)是定义在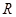 上的奇函数,且
上的奇函数,且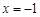 时,函数
时,函数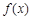 取极值1.
取极值1.
(Ⅰ)求函数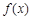 的解析式;
的解析式;
(Ⅱ)令 ,若
,若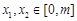 (
(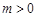 ),不等式
),不等式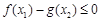 恒成立,求实数
恒成立,求实数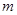 的取值范围;
的取值范围;
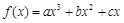 (
( )是定义在
)是定义在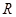 上的奇函数,且
上的奇函数,且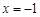 时,函数
时,函数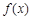 取极值1.
取极值1.(Ⅰ)求函数
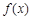 的解析式;
的解析式;(Ⅱ)令
 ,若
,若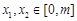 (
(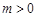 ),不等式
),不等式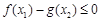 恒成立,求实数
恒成立,求实数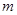 的取值范围;
的取值范围;(Ⅰ)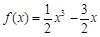 (Ⅱ)
(Ⅱ)
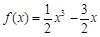 (Ⅱ)
(Ⅱ)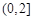
试题分析:(Ⅰ)函数
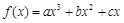 (
( )是定义在R上的奇函数,
)是定义在R上的奇函数,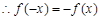 恒成立,即
恒成立,即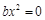 对于
对于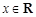 恒成立,
恒成立,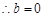 . 2分
. 2分则
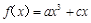 ,
,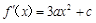 ,
,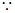
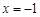 时,函数取极值1.∴
时,函数取极值1.∴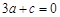 ,
,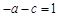 ,
,解得
 .∴
.∴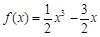 . 4分
. 4分(Ⅱ)不等式
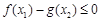 恒成立,只需
恒成立,只需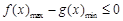 即可. 5分
即可. 5分∵函数
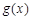 在
在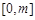 上单调递减,∴
上单调递减,∴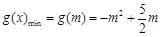 . 6分
. 6分又
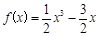 ,
,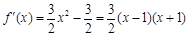 ,
,由
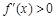 得
得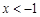 或
或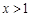 ;
;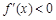 得
得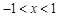 ,
,故函数
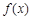 在
在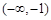 ,
,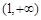 上单调递增,在
上单调递增,在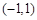 上单调递减,
上单调递减,则当
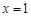 时,
时,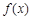 取得极小值, 8分
取得极小值, 8分在
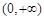 上,当
上,当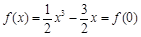 时,
时,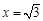 ,
,①当
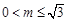 时,
时,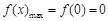 ,
,则
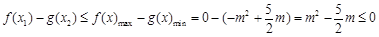 ,
,解得
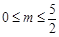 ,故此时
,故此时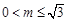 . 10分
. 10分②当
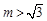 时,
时,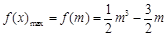 ,
,则
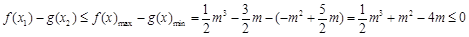 ,
,解得
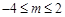 ,故此时
,故此时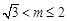 .综上所述,实数m的取值范围是
.综上所述,实数m的取值范围是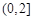 . 12分
. 12分点评:第一问中
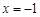 时,函数
时,函数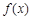 取极值1中隐含了两个关系式:
取极值1中隐含了两个关系式: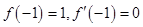 ;,第二问不等式恒成立问题求参数范围的,常转化为求函数最值问题,本题中要注意的是
;,第二问不等式恒成立问题求参数范围的,常转化为求函数最值问题,本题中要注意的是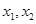 的取值范围是不同的,因此应分别求两函数最值
的取值范围是不同的,因此应分别求两函数最值
练习册系列答案
相关题目
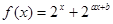 ,且
,且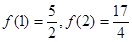
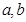 ;
;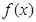 的奇偶性;
的奇偶性;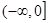 上的单调性,并证明。
上的单调性,并证明。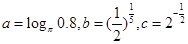 ,则有( )
,则有( )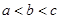
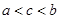
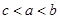

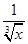 定义域相同的函数为( )
定义域相同的函数为( )


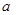 米的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少米?方盒的最大容积为多少?
米的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少米?方盒的最大容积为多少?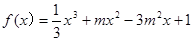 ,
,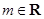 .
.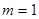 时,求曲线
时,求曲线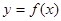 在点
在点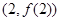 处的切线方程;
处的切线方程;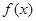 在区间
在区间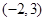 上是减函数,求
上是减函数,求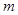 的取值范围.
的取值范围.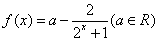
 的单调性;
的单调性; ,使函数
,使函数 ,
,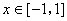 ,则
,则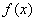 为偶函数,且在
为偶函数,且在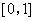 上单调递减
上单调递减 上单调递增
上单调递增 在下列定义域内的值域。
在下列定义域内的值域。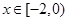 函数y=f(x)的值域
函数y=f(x)的值域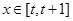 (其中
(其中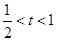 )函数y=f(x)的值域。
)函数y=f(x)的值域。