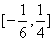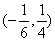题目内容
已知函数 ,
, .
.
(1)当 时,求曲线
时,求曲线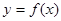 在点
在点 处的切线方程;
处的切线方程;
(2)若 在区间
在区间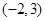 上是减函数,求
上是减函数,求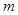 的取值范围.
的取值范围.
 ,
, .
.(1)当
 时,求曲线
时,求曲线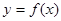 在点
在点 处的切线方程;
处的切线方程;(2)若
 在区间
在区间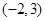 上是减函数,求
上是减函数,求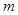 的取值范围.
的取值范围.(1)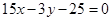 (2)
(2) 或
或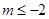 .
.
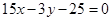 (2)
(2) 或
或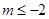 .
.试题分析:解:(1)当
 时,
时, ,又
,又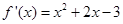 ,所以
,所以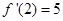 .
.又
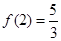 , 所以所求切线方程为
, 所以所求切线方程为 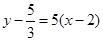 ,即
,即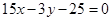 .
.所以曲线
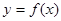 在点
在点 处的切线方程为
处的切线方程为 . 6分
. 6分(2)因为
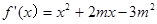 ,
,令
 ,得
,得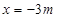 或
或 . 8分
. 8分当
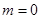 时,
时, 恒成立,不符合题意. 9分
恒成立,不符合题意. 9分当
 时,
时, 的单调递减区间是
的单调递减区间是 ,若
,若 在区间
在区间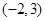 上是减函数,
上是减函数,则
 解得
解得 . 10分
. 10分当
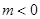 时,
时, 的单调递减区间是
的单调递减区间是 ,若
,若 在区间
在区间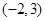 上是减函数,
上是减函数,则
 ,解得
,解得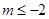 .
. 综上所述,实数
 的取值范围是
的取值范围是 或
或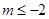 . 12分
. 12分点评:主要是考查了导数的几何意义的运用,以及运用导数判定函数单调性,属于中档题。

练习册系列答案
相关题目
 的图象如图所示,将
的图象如图所示,将 的图象向左平移
的图象向左平移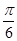 个单位,得到
个单位,得到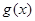 的图象,则函数
的图象,则函数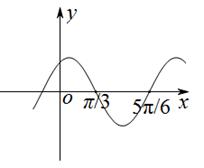
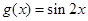
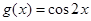
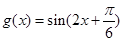
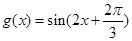
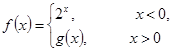 若
若 是奇函数,则
是奇函数,则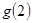 的值是( )
的值是( )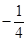

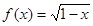 定义域为
定义域为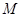 ,
,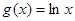 定义域为
定义域为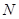 ,则
,则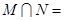 ( )
( )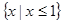
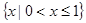
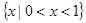
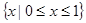
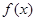 是以
是以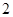 为周期的奇函数,若
为周期的奇函数,若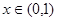 时,
时,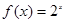 ,则
,则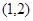 上是( )
上是( )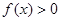
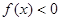
 (
(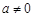 )是定义在
)是定义在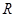 上的奇函数,且
上的奇函数,且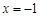 时,函数
时,函数 取极值1.
取极值1. ,若
,若 (
(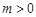 ),不等式
),不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;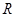 上的函数
上的函数 同时满足性质:①对任何
同时满足性质:①对任何 ,均有
,均有 成立;②对任何
成立;②对任何 ,当且仅当
,当且仅当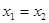 时,有
时,有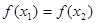 .则
.则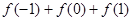 的值为 .
的值为 . 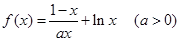
 时,求
时,求 在[1,
在[1,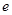 ]上的取值范围。
]上的取值范围。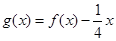 在[1,
在[1,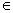 [0,1]时,f(x)=
[0,1]时,f(x)=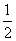 -x,若g(x)=f(x)-m(x+1)在区间(-1,2]有3个零点,则实数m的取值范围是
-x,若g(x)=f(x)-m(x+1)在区间(-1,2]有3个零点,则实数m的取值范围是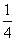 ,
,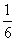 )
)