题目内容
对于函数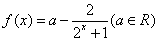
(1)探索函数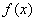 的单调性;
的单调性;
(2)是否存在实数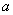 ,使函数
,使函数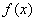 为奇函数?
为奇函数?
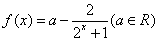
(1)探索函数
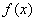 的单调性;
的单调性;(2)是否存在实数
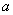 ,使函数
,使函数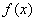 为奇函数?
为奇函数?(1)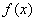 在
在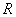 上是增函数(2)
上是增函数(2)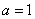 时,
时,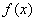 为奇函数
为奇函数
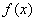 在
在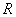 上是增函数(2)
上是增函数(2)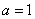 时,
时,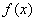 为奇函数
为奇函数试题分析:证明:(Ⅰ)解:(1)函数
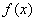 的定义域是R, 1分
的定义域是R, 1分设
 ,则
,则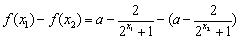
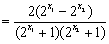 ,4分
,4分由
 ,
,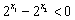 ,知
,知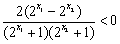 ,得
,得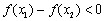 ,
, 所以
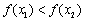 .
.故
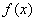 在
在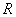 上是增函数. 6分
上是增函数. 6分(2)存在。
因为函数
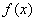 的定义域是R,故要使
的定义域是R,故要使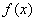 为奇函数,必有
为奇函数,必有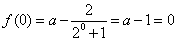 ,解得
,解得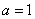 . 8分
. 8分下面证明当
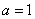 时,
时,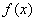 为奇函数。
为奇函数。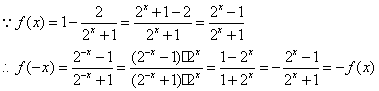 , 11分
, 11分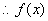 为奇函数。
为奇函数。由上可知,存在实数
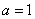 ,使
,使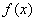 为奇函数。 12分
为奇函数。 12分点评:主要是考查了函数的性质的综合运用,属于中档题。

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
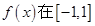 上是增函数,且
上是增函数,且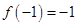 ,若函数
,若函数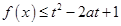 对所有的
对所有的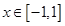 都成立,则当
都成立,则当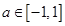 时t的取值范围是 ( )
时t的取值范围是 ( )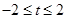
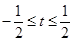
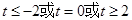
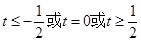
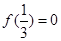 ,则不等式
,则不等式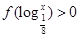 的解集是
的解集是 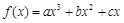 (
( )是定义在
)是定义在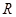 上的奇函数,且
上的奇函数,且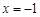 时,函数
时,函数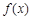 取极值1.
取极值1. ,若
,若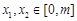 (
(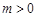 ),不等式
),不等式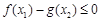 恒成立,求实数
恒成立,求实数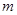 的取值范围;
的取值范围;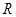 上的函数
上的函数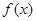 满足:
满足: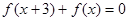 ,且函数
,且函数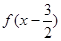 为奇函数。给出以下3个命题:
为奇函数。给出以下3个命题: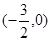 对称;
对称;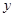 轴对称。
轴对称。

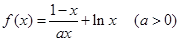
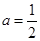 时,求
时,求 在[1,
在[1,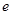 ]上的取值范围。
]上的取值范围。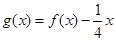 在[1,
在[1, .
. 时,求
时,求 的单调区间,如果函数
的单调区间,如果函数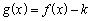 仅有两个零点,求实数
仅有两个零点,求实数 的取值范围;
的取值范围;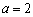 时,试比较
时,试比较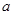 和
和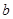 是先后抛掷该枚骰子得到的数字,函数
是先后抛掷该枚骰子得到的数字,函数
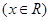
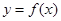 有零点的概率;
有零点的概率;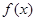 ,在使
,在使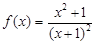 的下确界为_______________.
的下确界为_______________.