题目内容

7．对于函数f（x）=tex-x，若存在实数a，b（a＜b），使得f（x）≤0的解集为[a，b]，则实数t的取值范围是（0，$\frac{1}{e}$）．

分析 转化tex≤x，为t的不等式，求出表达式的最大值，以及单调区间，即可得到t的取值范围．

解答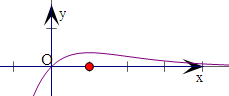
解：tex≤x（e是自然对数的底数），转化为t≤$\frac{x}{{e}^{x}}$，
令y=$\frac{x}{{e}^{x}}$，
则y′=$\frac{{e}^{x}-x{e}^{x}}{{e}^{2x}}$，令y′=0，可得x=1，
当x＞1时，y′＜0，函数y递减；当x＜1时，y′＞0，函数y递增．
则当x=1时函数y取得最大值$\frac{1}{e}$，
由于存在实数a、b，使得f（x）≤0的解集为[a，b]，
则由右边函数y=$\frac{x}{{e}^{x}}$的图象可得t的取值范围为（0，$\frac{1}{e}$）．
故答案为（0，$\frac{1}{e}$）．

点评 本题考查函数的导数的最值的应用，考查转化思想与计算能力．属于中档题．

练习册系列答案
相关题目
17．函数f（x）=2x+x-4的零点坐在的区间为（　　）
A．（-1，0）B．（0，1）C．（1，2）D．（2，3）
18．设O是坐标原点，F是抛物线y=x2的焦点，A是抛物线上的一点，FA与x轴正向的夹角为$\frac{π}{6}$，则|$\overrightarrow{AF}$|=（　　）
A．$\frac{1}{2}$B．$\frac{3}{4}$C．1D．2+$\sqrt{3}$
15．已知角A，B，C为△ABC的三个内角，那么$\frac{1}{2}$[cos（A-B）-cos（A+B）]sin2C的取值范围是（　　）
A．（0，$\frac{20}{27}$]B．（0，$\frac{16}{27}$]C．（0，$\frac{9}{16}$]D．（0，$\frac{7}{16}$]
2．设F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点，O为坐标原点，点A，B分别在双曲线的两条渐近线上，AF⊥x轴，BF∥OA，$\overrightarrow{AB}$•$\overrightarrow{OB}$=0，则该双曲线的离心率为$\frac{2\sqrt{3}}{3}$．
12．已知PA是圆O的切线，切点为A，PA=2，AC是圆O的直径，PC与圆O交于点B，PB=1，则AC=2$\sqrt{3}$．
19．执行如图所示的程序框图，则输出的S的值为（　　）
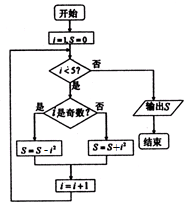
A．7B．8C．9D．10
16．已知集合M={ x|y=lg[（x-2）（x+1）]}，N={ y|y=$\sqrt{x+1}$}，全集为实数集R，则M∩N=（2，+∞），M∪N=（-∞，-1）∪[0，+∞），CRM=[-1，2]．
17．已知函数f（x）=sin（x+$\frac{π}{6}$）+cosx，x∈R，
（1）求函数f（x）的最大值，并写出当f（x）取得最大值时x的取值集合；
（2）若α∈（0，$\frac{π}{2}$），f（α+$\frac{π}{6}$）=$\frac{3\sqrt{3}}{5}$，求f（2α）的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网