Question

【题目】已知 ：方程 有两个不等的正根； ：方程 表示焦点在 轴上的双曲线.
（1）若 为真命题，求实数 的取值范围；
（2）若“ 或 ”为真，“ 且 ”为假，求实数 的取值范围

Answer 1

【答案】
（1）解：由已知方程 表示焦点在 轴上的双曲线，

所以 ，解得 ，即

（2）解：若方程 有两个不等的正根，

则 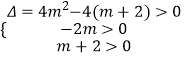解得 ，即 .

因 或 为真，所以 至少有一个为真.

又 且 为假，所以 至少有一个为假.

因此， 两命题应一真一假，当 为真， 为假时， ，解得 ；

当 为假， 为真时， ，解得 .

综上， 或 .

【解析】(1)根据题意结合已知条件焦点在 y 轴上的双曲线，即可得出关于m的不等式组解出m的取值范围即可。(2)利用题中条件当命题p为真命题时，借助二次函数根的情况以及韦达定理求出m的取值范围，结合题意由“ p 或 q ”为真，“ p 且 q ”为假可得出p 或 q 为真，所以 p 、 q 至少有一个为真.又 且 为假，所以 至少有一个为假，按照这两种情况分情况讨论即可的出m的取值范围。
【考点精析】通过灵活运用命题的真假判断与应用，掌握两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系即可以解答此题．