题目内容
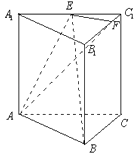
【题目】如图,在三棱锥 ![]() 中,
中, ![]() 平面
平面 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别在线段
分别在线段 ![]() 上,
上, ![]() ,
, ![]() ,
, ![]() 是
是 ![]() 的中点.
的中点.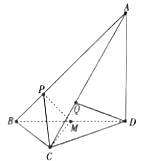
(1)证明: ![]() 平面
平面 ![]() ;
;
(2)若二面角 ![]() 的大小为
的大小为 ![]() ,求
,求 ![]() .
.
【答案】
(1)证明:取 ![]() 的中点
的中点 ![]() ,连接
,连接 ![]() ,则
,则 ![]() ,所以
,所以 ![]() .
.
又 ![]() 平面
平面 ![]() ,所以
,所以 ![]() 平面
平面 ![]() .
.
又 ![]() 是
是 ![]() 的中位线,所以
的中位线,所以 ![]() ,
,
从而 ![]() 平面
平面 ![]() .
.
又 ![]() ,所以平面
,所以平面 ![]() 平面
平面 ![]() .
.
因为 ![]() 平面
平面 ![]() ,所以
,所以 ![]() 平面
平面 ![]()
(2) 解:以 ![]() 为坐标原点,
为坐标原点, ![]() 所在的直线分别为
所在的直线分别为 ![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立如图所示的空间直角坐标.
轴建立如图所示的空间直角坐标.
设 ![]() ,
, ![]() ,则
,则 ![]() ,
, ![]() ,
, ![]() ,则
,则 ![]() ,
, ![]() ,
,
设 ![]() 是平面
是平面 ![]() 的一个法向量,
的一个法向量,
则  即
即 ![]() 取
取 ![]() ,
,
不难得到平面 ![]() 的一个法向量为
的一个法向量为 ![]() ,
,
所以 ![]() ,所以
,所以 ![]() ,
,
在 ![]() 中,
中, ![]() .
.

【解析】(1)根据题意作出辅助线利用对应线段成比例性质即可得出线线平行进而得到线面平行,再利用中位线的性质得到线线平行结合线面平行的判定定理即可得证。(2)根据题意建立空间直角坐标系,求出各个点的坐标进而求出各个向量的坐标,设出平面ABC和平面ABD的法向量,由向量垂直的坐标运算公式可求出法向量,再利用向量的数量积运算公式求出余弦值进而可得到二面角的正切值。
【考点精析】掌握直线与平面平行的判定和平面与平面平行的判定是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;判断两平面平行的方法有三种:用定义;判定定理;垂直于同一条直线的两个平面平行.

 阅读快车系列答案
阅读快车系列答案【题目】某商店对新引进的商品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
定价 | 9 | 9.2 | 9.4 | 9.6 | 9.8 | 10 |
销量 | 100 | 94 | 93 | 90 | 85 | 78 |
(1)求回归直线方程![]() ;
;
(2)假设今后销售依然服从(Ⅰ)中的关系,且该商品金价为每件5元,为获得最大利润,商店应该如何定价?(利润=销售收入-成本)
参考公式:![]() .
.