题目内容
如图,在半径为 、圆心角为60°的扇形的
、圆心角为60°的扇形的 弧上任取一点
弧上任取一点 ,作扇形的内接矩形
,作扇形的内接矩形 ,使点
,使点 在
在 上,点
上,点 在
在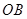 上,设矩形
上,设矩形 的面积为
的面积为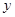 .
.
(Ⅰ) 按下列要求写出函数关系式:
① 设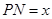 ,将
,将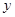 表示成
表示成 的函数关系式;
的函数关系式;
② 设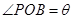 ,将
,将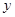 表示成
表示成 的函数关系式.
的函数关系式.
(Ⅱ) 请你选用(Ⅰ)中的一个函数关系式,求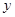 的最大值.
的最大值.
(Ⅰ)详见解析;(Ⅱ)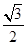 .
.
解析试题分析:(Ⅰ)①要用 表示矩形
表示矩形 的面积,关键是把
的面积,关键是把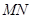 用
用 表示,在
表示,在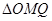 中可表示出
中可表示出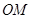 ,在
,在 中可表示出
中可表示出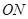 ,
,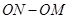 即得
即得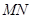 ;②在
;②在 中,可用
中,可用 表示
表示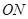 和
和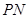 ,在在
,在在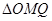 中可用
中可用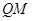 即
即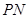 表示出
表示出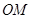 ,
,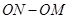 即得
即得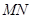 ;(Ⅱ)对(Ⅰ)中函数,是常见的函数或三角函数问题,较为容易解答,求出其最大值.
;(Ⅱ)对(Ⅰ)中函数,是常见的函数或三角函数问题,较为容易解答,求出其最大值.
试题解析:(Ⅰ) ① 因为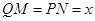 ,所以
,所以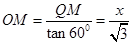 ,
,
又 ,所以
,所以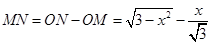 2分
2分
故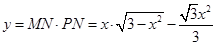 (
(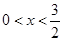 ) 4分
) 4分
② 当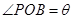 时,
时, 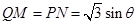 ,则
,则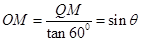 ,又
,又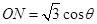 ,所以
,所以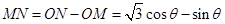 6分
6分
故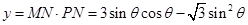 (
(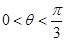 ) 8分
) 8分
(Ⅱ)由②得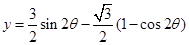 =
=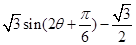 12分
12分
故当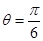 时,
时,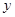 取得最大值为
取得最大值为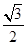 15分
15分
考点:函数的应用、三角函数.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 三个内角A,B,C所对的边,向量
三个内角A,B,C所对的边,向量 ,设
,设
 ,求角
,求角 ;
; ,求三角形ABC的面积.
,求三角形ABC的面积.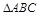 中,
中, 分别是角
分别是角 的对边,
的对边, ,
, ;
; 的值;
的值; ,求边
,求边 的长.
的长. 是锐角三角形,
是锐角三角形, 分别是内角
分别是内角 所对边长,并且
所对边长,并且 .
. 的值;
的值; ,求
,求 (其中
(其中 ).
). 的图象过点(0,
的图象过点(0, ),最小正周期为
),最小正周期为 ,且最小值为-1.
,且最小值为-1. 的解析式.
的解析式. ,
, ,求m的取值范围.
,求m的取值范围. 中,内角
中,内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,已知
,已知 .
. 的值;
的值; ,求
,求 为
为 的内角
的内角 的对边,满足
的对边,满足 ,函数
,函数
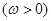 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减.
上单调递减. ;
; ,证明
,证明
 的值;
的值; 且
且 ,
, ,求
,求
 的值。
的值。 sin20°cos80°的值.
sin20°cos80°的值.