题目内容
设 是锐角三角形,
是锐角三角形, 分别是内角
分别是内角 所对边长,并且
所对边长,并且 .
.
(1)求角 的值;
的值;
(2)若 ,求
,求 (其中
(其中 ).
).
(1) 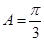 ;(2)
;(2) 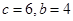 .
.
解析试题分析:(1) 利用两角和与差的正弦公式展开化简得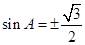 ,又
,又 为锐角,所以
为锐角,所以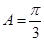 ;(2)由
;(2)由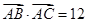 可得
可得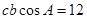 ,即
,即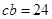 ,然后利用余弦定理
,然后利用余弦定理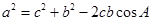 得
得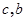 的另一个关系,从而解出
的另一个关系,从而解出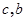 .
.
试题解析:(1)因为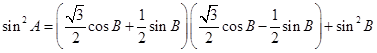
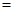
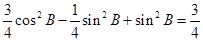 ,
,
所以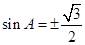 ,又
,又 为锐角,所以
为锐角,所以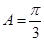 .
.
(2)由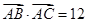 可得
可得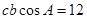 ①
①
由(1)知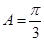 ,所以
,所以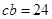 ②
②
由余弦定理知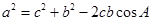 ,将
,将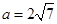 及①代入,得
及①代入,得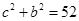 ③
③
③+②×2,得 ,所以
,所以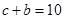
因此,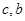 是一元二次方程
是一元二次方程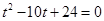 的两个根.
的两个根.
解此方程并由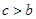 知
知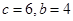 .
.
考点:两角和与差的正弦定理、平面向量的数量积、余弦定理.

练习册系列答案
相关题目
 .
. 的最大值及取得最大值时x的值;
的最大值及取得最大值时x的值; ,
,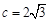 ,
, ,求△ABC的面积.
,求△ABC的面积. 且对
且对 是常数,
是常数, .
. 的值;
的值;

 ,
,
 时,求函数
时,求函数 的值域;
的值域;
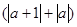 ,当
,当 时恒成立,求
时恒成立,求 的取值范围.
的取值范围. 、圆心角为60°的扇形的
、圆心角为60°的扇形的 弧上任取一点
弧上任取一点 ,作扇形的内接矩形
,作扇形的内接矩形 ,使点
,使点 在
在 上,点
上,点 在
在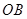 上,设矩形
上,设矩形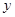 .
.
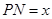 ,将
,将 的函数关系式;
的函数关系式;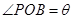 ,将
,将 的函数关系式.
的函数关系式.
 最小正周期及单调递增区间;
最小正周期及单调递增区间; 时,求
时,求 且
且 ,求:
,求: 的值.
的值. ,tanα=
,tanα= ,求:
,求: 的值.
的值. (2)
(2) .
.