题目内容
(本小题满分14分)
某造船公司年最高造船量是20艘. 已知造船x艘的产值函数为R(x)="3700x" + 45x2 – 10x3(单位:万元), 成本函数为C (x) =" 460x" + 5000 (单位:万元). 又在经济学中,函数f(x)的边际函数Mf (x)定义为: Mf (x) =" f" (x+1) – f (x). 求:
(1) 利润函数P(x) 及边际利润函数MP(x);
(2) 年造船量安排多少艘时, 可使公司造船的年利润最大?
(3) 边际利润函数MP(x)的单调递减区间, 并说明单调递减在本题中的实际意义是什么?
某造船公司年最高造船量是20艘. 已知造船x艘的产值函数为R(x)="3700x" + 45x2 – 10x3(单位:万元), 成本函数为C (x) =" 460x" + 5000 (单位:万元). 又在经济学中,函数f(x)的边际函数Mf (x)定义为: Mf (x) =" f" (x+1) – f (x). 求:
(1) 利润函数P(x) 及边际利润函数MP(x);
(2) 年造船量安排多少艘时, 可使公司造船的年利润最大?
(3) 边际利润函数MP(x)的单调递减区间, 并说明单调递减在本题中的实际意义是什么?
(1)MP (x) =" P" ( x + 1 ) – P (x) =" –" 30x2 + 60x +3275 (xÎN且xÎ[1, 20])
(2)年建造12艘船时, 公司造船的年利润最大
(3)MP (x)是减函数说明: 随着产量的增加,每艘利润与前一台比较,利润在减少
(1) P(x) =" R" (x) – C (x) =" –" 10x3 + 45x2 + 3240x – 5000 (xÎN且xÎ[1, 20]); 3分
MP (x) =" P" ( x + 1 ) – P (x) =" –" 30x2 + 60x +3275 (xÎN且xÎ[1, 20]). 2分
(2) P`(x) =" –" 30x2 + 90x + 3240 =" –" 30( x +9 )(x – 12) (xÎN且xÎ[1, 20]) 3分
当1£ x < 12时, P`(x) > 0, P(x)单调递增,
当 12 <x £ 20时, P`(x) < 0 , P ( x ) 单调递减.
∴ x =" 12" 时, P(x)取最大值,
即, 年建造12艘船时, 公司造船的年利润最大. 4分
(3) 由MP(x ) =" " – 30( x – 1) 2 + 3305 (xÎN且xÎ[1, 20]).
∴当1< x £ 20时,MP (x)单调递减. 1分
MP (x)是减函数说明: 随着产量的增加,每艘利润与前一台比较,利润在减少.1分
MP (x) =" P" ( x + 1 ) – P (x) =" –" 30x2 + 60x +3275 (xÎN且xÎ[1, 20]). 2分
(2) P`(x) =" –" 30x2 + 90x + 3240 =" –" 30( x +9 )(x – 12) (xÎN且xÎ[1, 20]) 3分
当1£ x < 12时, P`(x) > 0, P(x)单调递增,
当 12 <x £ 20时, P`(x) < 0 , P ( x ) 单调递减.
∴ x =" 12" 时, P(x)取最大值,
即, 年建造12艘船时, 公司造船的年利润最大. 4分
(3) 由MP(x ) =" " – 30( x – 1) 2 + 3305 (xÎN且xÎ[1, 20]).
∴当1< x £ 20时,MP (x)单调递减. 1分
MP (x)是减函数说明: 随着产量的增加,每艘利润与前一台比较,利润在减少.1分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
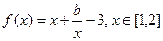
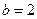 时,求
时,求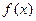 的值域;
的值域;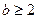 时,
时,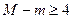 ,求b的取值范围.
,求b的取值范围.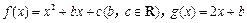 ,且对于任意
,且对于任意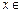 R,恒有
R,恒有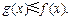
 ;
;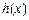 满足:
满足: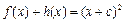 ,证明:函数
,证明:函数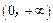 内没有零点.
内没有零点.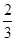 倍,且对每个项目的投资不能低于5万元;对甲项目每投资1万元可获得0.4万元的利润,对乙项目每投资1万元可获得0.6万元的利润,如该公司在正确规划后,在这两个项目上共可获得的最大利润为 万元。
倍,且对每个项目的投资不能低于5万元;对甲项目每投资1万元可获得0.4万元的利润,对乙项目每投资1万元可获得0.6万元的利润,如该公司在正确规划后,在这两个项目上共可获得的最大利润为 万元。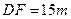 的吊车,吊车底座
的吊车,吊车底座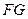 高
高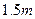 ,现准备把一个底半径为
,现准备把一个底半径为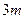 高
高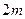 的圆柱形工件吊起平放到
的圆柱形工件吊起平放到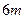 高的桥墩上,问能否将工件吊到桥墩上?(参考数据:
高的桥墩上,问能否将工件吊到桥墩上?(参考数据: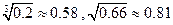 )
)
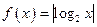 ,当
,当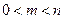 时,有
时,有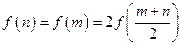 .
.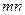 的值;
的值;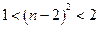
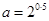 ,
,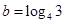 ,
,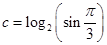 ,则
,则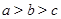
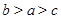
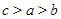
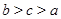
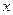 的方程
的方程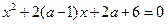 有一正一负两实根,实数
有一正一负两实根,实数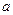 取值范围__
取值范围__