题目内容
15.集合M={x∈Q|-2≤x≤1},N={x∈R|-1≤x≤2},则M∩N={x∈Q|-1≤x≤1},M∪N={x∈R|-2≤x≤2}.分析 直接由交集、并集的运算得答案.
解答 解:∵M={x∈Q|-2≤x≤1},N={x∈R|-1≤x≤2},
∴M∩N={x∈Q|-2≤x≤1}∩{x∈R|-1≤x≤2}={x∈Q|-1≤x≤1};
M∪N={x∈Q|-2≤x≤1}∪{x∈R|-1≤x≤2}={x∈R|-2≤x≤2}.
故答案为:{x∈Q|-1≤x≤1},{x∈R|-2≤x≤2}.
点评 本题考查了交集、并集的运算,是基础的概念题.

练习册系列答案
相关题目
10.命题“对任意的x∈R,x2≥0”的否定是( )
| A. | 对任意的x∈R,x2<0 | B. | 不存在x∈R,x2<0 | ||
| C. | 存在x∈R,x2<0 | D. | 存在x∈R,x2≥0 |
7.下列函数中,既是偶函数,又在区间(1,2)内是增函数的为( )
| A. | y=cos2x,x∈R | B. | y=x3+1,x∈R | ||
| C. | y=$\frac{{e}^{x}-{e}^{-x}}{2}$,x∈R | D. | y=log2|x|,x∈R且x≠0 |
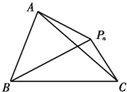 如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3:1,$\overrightarrow{{P_n}A}$=$\frac{{{x_{n+1}}}}{3}$$\overrightarrow{{P_n}B}$-(2xn+1)$\overrightarrow{{P_n}C}$(其中,{xn}是首项为1的正项数列),则x4等于( )
如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3:1,$\overrightarrow{{P_n}A}$=$\frac{{{x_{n+1}}}}{3}$$\overrightarrow{{P_n}B}$-(2xn+1)$\overrightarrow{{P_n}C}$(其中,{xn}是首项为1的正项数列),则x4等于( )