题目内容
20．函数f（x）=x2-ax-a在区间[0，2]上的最大值为1，则实数a=1．分析 根据函数f（x）=x2-ax-a的图象为开口向上的抛物线，所以函数的最大值在区间的端点取得，利用函数f（x）=x2-ax-a在区间[0，2]上的最大值为1，可求实数a的值．
解答 解：∵函数f（x）=x2-ax-a的图象为开口向上的抛物线，
∴函数的最大值在区间的端点取得，
∵f（0）=-a，f（2）=4-3a，
∴$\left\{\begin{array}{l}-a＞4-3a\\-a=1\end{array}\right.$或$\left\{\begin{array}{l}-a＜4-3a\\ 4-3a=1\end{array}\right.$，
解得a=1，
∴实数a等于1，
故答案为：1
点评 本题考查的知识点是二次函数的图象图象和性质，熟练掌握二次函数的图象和性质，是解答的关键．
练习册系列答案
相关题目
11．下列函数中，既是奇函数又在[0，1]上单调递增的是（ ）
| A． | y=|x|•x3 | B． | y=xlnx | C． | y=x•cosx | D． | $y=-x-\frac{1}{x}$ |
8．函数f（x）=2x2-2x的单调递增区间是（ ）
| A． | （-∞，1] | B． | [1，+∞） | C． | （-∞，2] | D． | [2，+∞） |
5．设m，n是两条不同的直线，α，β，γ是三个不同的平面，则下面结论中正确的是（ ）
| A． | 若α⊥γ，β⊥γ，则α∥β | B． | 若m⊥n，m⊥α，n∥β，则α∥β | ||
| C． | 若m⊥α，m⊥β，则α∥β | D． | 若m∥n，m∥α，n∥β，则α∥β |
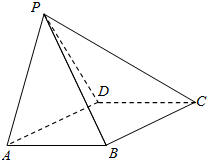如图所示，在四棱锥P-ABCD中，四边形ABCD为菱形，∠DAB=60°，AB=2，△PAD为等边三角形，平面PAD⊥平面ABCD．