题目内容
【题目】在数列{an}中,a1=2,an+1=4an﹣3n+1,n∈N*
(1)证明数列{an﹣n}为等比数列
(2)求数列{an}的前n项和Sn .
【答案】
(1)证明:∵an+1=4an﹣3n+1,n∈N*,
∴an+1﹣(n+1)=4an﹣3n+1﹣(n+1),
4an﹣4n=4(an﹣n).
∴{an﹣n}为首项a1﹣1=1,公比q=4的等比数列;
(2)解:∵an﹣n=4n﹣1,
∴an=n+4n﹣1,
Sn=1+2+…+n+(1+4+…+4n﹣1)= ![]() =
= ![]() .
.
【解析】(1)由an+1=4an﹣3n+1可得an+1﹣(n+1)=4an﹣3n+1﹣(n+1)=4an﹣4n=4(an﹣n),从而可证(2)由(1)可求an , 利用分组求和及等差数列与等比数列的求和公式可求Sn
【考点精析】掌握等差数列的前n项和公式和等比数列的前n项和公式是解答本题的根本,需要知道前n项和公式:![]() ;前
;前![]() 项和公式:
项和公式: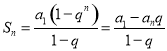 .
.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案【题目】某公司购买了A,B,C三种不同品牌的电动智能送风口罩.为了解三种品牌口罩的电池性能,现采用分层抽样的方法,从三种品牌的口罩中抽出25台,测试它们一次完全充电后的连续待机时长,统计结果如下(单位:小时):
A | 4 | 4 | 4.5 | 5 | 5.5 | 6 | 6 | |||
B | 4.5 | 5 | 6 | 6.5 | 6.5 | 7 | 7 | 7.5 | ||
C | 5 | 5 | 5.5 | 6 | 6 | 7 | 7 | 7.5 | 8 | 8 |
(Ⅰ)已知该公司购买的C品牌电动智能送风口罩比B品牌多200台,求该公司购买的B品牌电动智能送风口罩的数量;
(Ⅱ)从A品牌和B品牌抽出的电动智能送风口罩中,各随机选取一台,求A品牌待机时长高于B品牌的概率;
(Ⅲ)再从A,B,C三种不同品牌的电动智能送风口罩中各随机抽取一台,它们的待机时长分别是a,b,c(单位:小时).这3个新数据与表格中的数据构成的新样本的平均数记为![]() ,表格中数据的平均数记为
,表格中数据的平均数记为![]() .若
.若![]() ,写出a+b+c的最小值(结论不要求证明).
,写出a+b+c的最小值(结论不要求证明).
