题目内容
成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列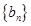 中的
中的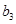 、
、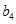 、
、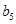 .
.
(1)求数列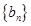 的通项公式;
的通项公式;
(2)数列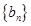 的前n项和为
的前n项和为 ,求证:数列
,求证:数列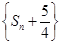 是等比数列.
是等比数列.
(1)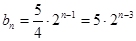 (2)证明过程见试题解析.
(2)证明过程见试题解析.
解析试题分析:(1)设成等差数列的三个正数分别为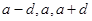 ,可得
,可得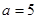 ,又
,又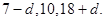 成等比,可得方程
成等比,可得方程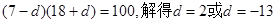 ,则等比数列的三项进一步求公比,可得通项公式.(2)等比数列
,则等比数列的三项进一步求公比,可得通项公式.(2)等比数列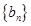 前n项和为
前n项和为 ,由
,由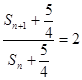 可知数列
可知数列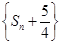 是等比数列.
是等比数列.
试题解析:解:(1)设成等差数列的三个正数分别为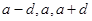
依题意,得
所以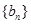 中的
中的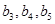 依次为
依次为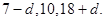
依题意,有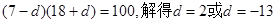 (舍去)
(舍去)
故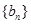 的第3项为5,公比为2.
的第3项为5,公比为2.
由
所以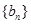 是以
是以 为首项,2为以比的等比数列,其通项公式为
为首项,2为以比的等比数列,其通项公式为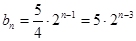 6分
6分
(2)数列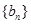 的前
的前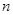 项和
项和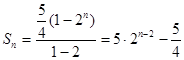 ,即
,即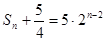
所以
所以,数列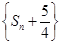 是等比数列. 12分
是等比数列. 12分
考点:等差数列定义,等比数列的定义,等比数列的前n项和公式.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
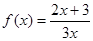 , 数列
, 数列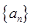 满足
满足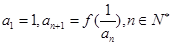 .
. ,若
,若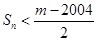 对一切
对一切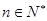 成立,求最小正整数m.
成立,求最小正整数m. 的前n项和为
的前n项和为 ,
,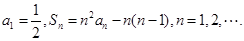
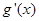 ;
;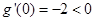 ,求证:
,求证: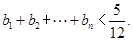
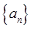 的前
的前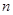 项和为
项和为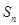 ,
,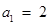 ,
,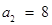 ,
, ,
,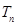 是数列
是数列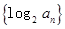 的前
的前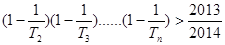 的最大正整数
的最大正整数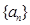 中抽出一些项,依原来的顺序组成的新数列叫数列
中抽出一些项,依原来的顺序组成的新数列叫数列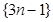 的一个是等比数列的子列;
的一个是等比数列的子列;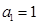 ,公比为
,公比为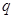 .求证:当
.求证:当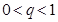 时,数列
时,数列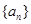 中,已知
中,已知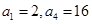 .
.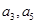 分别为等差数列
分别为等差数列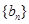 的第3项和第5项,试求数列
的第3项和第5项,试求数列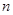 项和
项和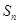 。
。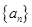 中,
中,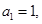 且对任意的
且对任意的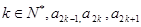 成等比数列,其公比为
成等比数列,其公比为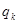 ,
,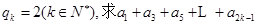 ;
;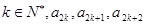 成等差数列,其公差为
成等差数列,其公差为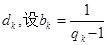 .
.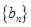 成等差数列,并指出其公差;
成等差数列,并指出其公差;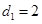 ,试求数列
,试求数列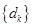 的前
的前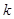 项和
项和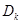 .
.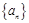 的前n项和为Sn,已知
的前n项和为Sn,已知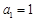 ,且
,且 对一切
对一切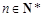 都成立.
都成立.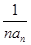 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.