题目内容
已知函数f(x)=sinx,g(x)=cos2x,以下判断正确的序号是
(1)函数h(x)=f(x)-tanx在x∈(-
,0]上的零点只有1个.
(2)函数h(x)=f(x+1)-
在x∈(1,2π)上的零点只有1个.
(3)函数h(x)=
f(x)+g(x)+a在x∈[0,π]的零点个数为1个时,a无解
(4)函数h(x)=
f(x)+g(x)+a在x∈[0,π]的零点个数为2时,a∈(-1,-
)∪{-
}.
(1)函数h(x)=f(x)-tanx在x∈(-
| π |
| 2 |
(2)函数h(x)=f(x+1)-
| π |
| 2x+2 |
(3)函数h(x)=
| 1 |
| 2 |
(4)函数h(x)=
| 1 |
| 2 |
| 1 |
| 2 |
| 17 |
| 16 |
考点:命题的真假判断与应用
专题:计算题,阅读型,函数的性质及应用,三角函数的图像与性质
分析:运用零点的定义,解方程,即可判断(1);运用导数判断函数的单调性,即可判断零点个数,可判断(2);令h(x)=0,运用同角公式和正弦函数的性质,即可判断(3)、(4).
解答:
解:对于(1),由sinx=tanx,即有sinx=0或cosx=1,在x∈(-
,0]上只有x=0,则(1)对;
对于(2),h(x)=sin(x+1)-
,h′(x)=cos(x+1)+
,由于1<x<2π,h′(x)=0有解,则h(x)不单调,则零点不唯一,则(2)错;
对于(3),h(x)=
sinx+cos2x+a,令h(x)=0,则sin2x-
sinx=1+a,即(sinx-
)2=a+
,
由于0≤x≤π,则sinx∈[0,1],若h(x)零点个数为1,则x=
,此时a=-
,则(3)错;
对于(4),由(sinx-
)2=a+
,由于0≤x≤π,则sinx∈[0,1],sinx-
∈[-
,
],
若h(x)零点个数为2,即有0≤
<
,且-
<-
,解得,-1<a<-
或a=-
.则④对.
故答案为:(1)(4).
| π |
| 2 |
对于(2),h(x)=sin(x+1)-
| π |
| 2x+2 |
| π |
| 2(x+1)2 |
对于(3),h(x)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 17 |
| 16 |
由于0≤x≤π,则sinx∈[0,1],若h(x)零点个数为1,则x=
| π |
| 2 |
| 1 |
| 2 |
对于(4),由(sinx-
| 1 |
| 4 |
| 17 |
| 16 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
若h(x)零点个数为2,即有0≤
a+
|
| 3 |
| 4 |
a+
|
| 1 |
| 4 |
| 1 |
| 2 |
| 17 |
| 16 |
故答案为:(1)(4).
点评:本题考查函数的零点的判断和求法,考查函数的性质和运用,考查运算能力,属于中档题和易错题.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
函数y=2x-x2的图象大致是( )
A、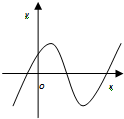 |
B、 |
C、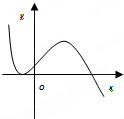 |
D、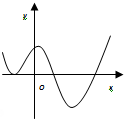 |