题目内容
在空间四边形ABCD中，E、F分别是AB、BC上的中点，G属于CD、H属于AD，EH与FG相交于点P，求证：交点P必在直线BD上．
考点：平面的基本性质及推论
专题：计算题,空间位置关系与距离
分析：证明P属于平面BCD，同理点P属于平面ABD，所以点P必在平面BCD与平面ABD的交线上，即可证明结论．
解答：
证明：因为EH属于平面BCD，所以P属于平面BCD．
同理点P属于平面ABD，
所以点P必在平面BCD与平面ABD的交线上，
因为平面BCD与平面ABD的交线为BD，
所以交点P必在直线BD上．
同理点P属于平面ABD，
所以点P必在平面BCD与平面ABD的交线上，
因为平面BCD与平面ABD的交线为BD，
所以交点P必在直线BD上．
点评：本题考查平面的基本性质，考查学生分析解决问题的能力，比较基础．
练习册系列答案
相关题目
函数y=2x-x2的图象大致是（ ）
A、 |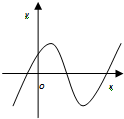
B、 |
C、 |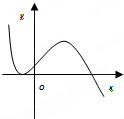
D、 |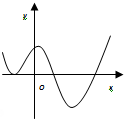
设a，b是不同的直线，α，β是不同的平面，则下列结论错误的是（ ）
| A、若a⊥α，b∥α，则a⊥b |
| B、若a⊥α，b⊥α，则a∥b |
| C、若b∥α，b?β，则α∥β |
| D、若a⊥α，a⊥β，则α∥β |
如图，Rt△O′A′B′是一平面图形的直观图，斜边O′B′=2，则这个平面图形的面积是（ ）
A、
| ||||
| B、1 | ||||
C、
| ||||
D、2
|
某校在一次趣味运动会的颁奖仪式上，高一、高二、高三各代表队人数分别为120人、120人、n人，为了活跃气氛，大会组委会在颁奖过程中穿插抽奖活动，并用分层抽样的方法从三个代表队中共抽取20人在前排就坐，其中高二代表队抽6人．