题目内容
20.设x,y满足约束条件$\left\{\begin{array}{l}{x+2y-2≥0}\\{x-y+1≥0}\\{2x-y-2≥0}\end{array}\right.$,则z=3x-y的取值范围是( )| A. | [-1,$\frac{16}{5}$] | B. | [-1,5] | C. | [$\frac{16}{5}$,+∞) | D. | [5,+∞) |
分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.
解答  解:由约束条件$\left\{\begin{array}{l}{x+2y-2≥0}\\{x-y+1≥0}\\{2x-y-2≥0}\end{array}\right.$作出可行域如图,
解:由约束条件$\left\{\begin{array}{l}{x+2y-2≥0}\\{x-y+1≥0}\\{2x-y-2≥0}\end{array}\right.$作出可行域如图,
联立$\left\{\begin{array}{l}{x+2y-2=0}\\{2x-y-2=0}\end{array}\right.$,解得:A($\frac{6}{5},\frac{2}{5}$),
由z=3x-y,得y=3x-z,
∴当直线y=3x-z过A($\frac{6}{5},\frac{2}{5}$)时,直线在y轴上的截距最大,z有最小值为$\frac{16}{5}$.
∴z=3x-y的取值范围是[$\frac{16}{5},+∞$).
故选:C.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
11.等比数列{an}的各项均为正数,且a5a6+a4a7=18,则log3a1+log3a2+…+log3a10=( )
| A. | 5 | B. | 9 | C. | log345 | D. | 10 |
15.cos2$\frac{π}{8}-{sin^2}\frac{π}{8}$的值为( )
| A. | -$\frac{{\sqrt{3}}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
12.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{3}(x-1),x>1}\\{{3}^{x}+2,x≤1}\end{array}\right.$则f(f(log32))的值是( )
| A. | 1 | B. | 2 | C. | 5 | D. | 1+log32 |
10.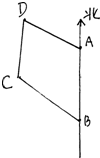 如图,海岸线上相距5海里的两座灯塔A、B,灯塔B位于A的正南方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向与A相距$3\sqrt{2}$海里的D处,乙船位于灯塔B的北偏西60°方向与B相距5海里的C处,则两艘轮船相距( )海里.
如图,海岸线上相距5海里的两座灯塔A、B,灯塔B位于A的正南方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向与A相距$3\sqrt{2}$海里的D处,乙船位于灯塔B的北偏西60°方向与B相距5海里的C处,则两艘轮船相距( )海里.
 如图,海岸线上相距5海里的两座灯塔A、B,灯塔B位于A的正南方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向与A相距$3\sqrt{2}$海里的D处,乙船位于灯塔B的北偏西60°方向与B相距5海里的C处,则两艘轮船相距( )海里.
如图,海岸线上相距5海里的两座灯塔A、B,灯塔B位于A的正南方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向与A相距$3\sqrt{2}$海里的D处,乙船位于灯塔B的北偏西60°方向与B相距5海里的C处,则两艘轮船相距( )海里.| A. | $2\sqrt{3}$ | B. | $\sqrt{13}$ | C. | $3\sqrt{2}$ | D. | $2\sqrt{5}$ |
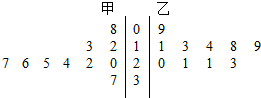 市体育运动学校的甲、乙两名篮球运动员练习投篮,每人练习10次,每次投篮40个.命中个数的茎叶图如下.则投篮命中率较高的运动员是甲.
市体育运动学校的甲、乙两名篮球运动员练习投篮,每人练习10次,每次投篮40个.命中个数的茎叶图如下.则投篮命中率较高的运动员是甲.