题目内容
已知函数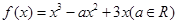 .
.
(1)若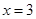 是
是 的极值点,求
的极值点,求 及
及 在
在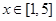 上的最大值;
上的最大值;
(2)若函数 是
是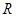 上的单调递增函数,求实数
上的单调递增函数,求实数 的取值范围.
的取值范围.
(1)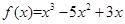 ,
, 在
在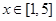 上的最大值为15;
上的最大值为15;
(2)实数 的取值范围为:
的取值范围为: .
.
解析试题分析:(1)先对函数求导,再把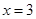 代入导函数使之为0,即解得
代入导函数使之为0,即解得 的值,进一步可求
的值,进一步可求 ;令导函数为0,列表可求
;令导函数为0,列表可求 在
在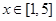 上的最大值;(2)函数
上的最大值;(2)函数 是
是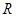 上的单调递增函数可转化为
上的单调递增函数可转化为 在R上恒成立,即可求出实数
在R上恒成立,即可求出实数 的取值范围.
的取值范围.
试题解析:(1) ,令
,令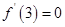 ,即
,即 ∴
∴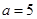 .
.
∴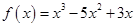 4分
4分
令 ,解得
,解得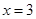 或
或 (舍去).
(舍去).
当 变化时,
变化时, ,
, ,的变化情况如下表:
,的变化情况如下表:
因此,当 
1 (1,3) 3 (3,5) 5 
0 + 
1 单调递减↘ 9 单调递增↗ 15 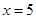 时,
时, 在区间[1,5]上有最大值是
在区间[1,5]上有最大值是 . 8分
. 8分
(2)  是R上的单调递增函数转化为
是R上的单调递增函数转化为 在R上恒成立, 10分
在R上恒成立, 10分
从而有 ,由
,由 ,解得
,解得

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
 ,(
,( >0,
>0, ,以点
,以点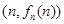 为切点作函数
为切点作函数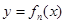 图象的切线
图象的切线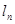 ,记函数
,记函数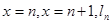 所围成的区域面积为
所围成的区域面积为 .
.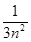 ;
;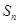 为数列
为数列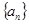 的前
的前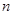 项和,求证:
项和,求证: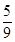 .来
.来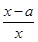 (a≠0).
(a≠0).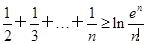 (e为自然对数的底数);
(e为自然对数的底数);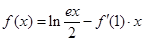 ,
,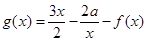 (其中
(其中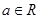 ).
). 的单调区间;
的单调区间;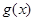 在区间
在区间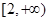 上为增函数,求
上为增函数,求 的取值范围;
的取值范围;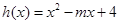 ,当
,当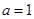 时,若存在
时,若存在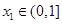 ,对任意的
,对任意的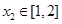 ,总有
,总有 成立,求实数
成立,求实数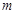 的取值范围.
的取值范围. 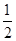 ax2-(2a+1)x+2ln x,a∈R.
ax2-(2a+1)x+2ln x,a∈R. 图像过点
图像过点 ,且在
,且在 处的切线方程是
处的切线方程是 .
. 的解析式;
的解析式; 上的最大值和最小值.
上的最大值和最小值.