题目内容
已知函数f(x)=ln ax-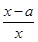 (a≠0).
(a≠0).
(1)求函数f(x)的单调区间及最值;
(2)求证:对于任意正整数n,均有1+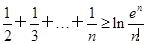 (e为自然对数的底数);
(e为自然对数的底数);
(3)当a=1时,是否存在过点(1,-1)的直线与函数y=f(x)的图象相切?若存在,有多少条?若不存在,请说明理由.
(1)当a>0时,函数在(0,a)上是减函数,在(a,+∞)上是增函数,f(x)min=f(a)=ln a2,无最大值.当a<0时,函数在(-∞,a)上是减函数,在(a,0)上是增函数,f(x)min=f(a)=ln a2,无最大值.(2)见解析(3)仅有一根
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在点(1,0)处的切线.
在点(1,0)处的切线. .其中
.其中 .
. 的值;
的值; ,若
,若 ,求
,求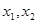
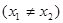 是函数
是函数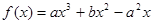 (
(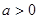 )的两个极值点
)的两个极值点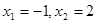 ,求函数
,求函数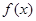 的解析式;
的解析式;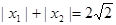 ,求
,求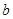 的最大值。
的最大值。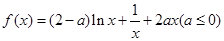 .
.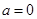 时,求
时,求 的极值;
的极值;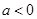 时,讨论
时,讨论 ,
,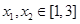 ,恒有
,恒有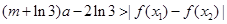 成立,求实数
成立,求实数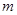 的取值范围.
的取值范围.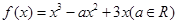 .
.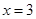 是
是 的极值点,求
的极值点,求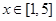 上的最大值;
上的最大值;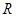 上的单调递增函数,求实数
上的单调递增函数,求实数 的取值范围.
的取值范围.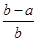 <ln
<ln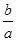 <
<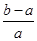 ,其中0<a<b;
,其中0<a<b; + +
+ + ]≤1+[lnn](n∈N*).
]≤1+[lnn](n∈N*).