Question

【题目】已知圆：内一点，点为圆上任意一点，线段的垂直平分线与线段连线交于点.

（1）求点的轨迹方程；

（2）设点的轨迹为曲线，过点的直线与曲线交于不同的两点、，求的内切圆半径的最大值.

Answer 1

【答案】（1）；（2）

【解析】

（1）根据线段中垂线的性质可得，|MP|＝|MQ|，又|MQ|＋|M|＝4，故有|M|＋|MP|＝4＞|P|，根据椭圆的定义判断轨迹椭圆，求出值，即得椭圆的标准方程；

（2）设，，设的内切圆的半径为，当最大，就最大，利用直线和椭圆的位置关系求出最大值，进而可得的最大值.

（1）由圆的方程可知，圆心（1，0），半径等于4，设点M的坐标为，
∵PQ的垂直平分线交Q于M，
∴|MP|＝|MQ|．
又|MQ|＋|M|＝4（半径），
∴|M|＋|MP|＝4＞|A|＝2．
∴点M满足椭圆的定义，且2＝4，2＝2，
∴＝2，＝1，
，
∴点M的轨迹方程为；

（2）设，，设的内切圆的半径为，因为的周长为，，因此最大，就最大，

，由题意知，直线的斜率不为零，可设直线的方程为，

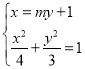由得，

所以，，

又因直线与椭圆交于不同的两点，故，即，，则，

令，则，

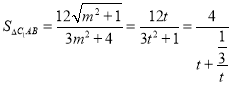，令，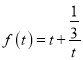

由函数的性质可知，函数在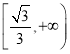上是单调递增函数，即当时，在上单调递增，因此有，所以，

即当，时，最大，此时，故当直线的方程为时，内切圆半径的最大值为.