题目内容
【题目】某乐园按时段收费,收费标准为:每玩一次不超过![]() 小时收费10元,超过
小时收费10元,超过![]() 小时的部分每小时收费
小时的部分每小时收费![]() 元(不足
元(不足![]() 小时的部分按
小时的部分按![]() 小时计算).现有甲、乙二人参与但都不超过
小时计算).现有甲、乙二人参与但都不超过![]() 小时,甲、乙二人在每个时段离场是等可能的。为吸引顾客,每个顾客可以参加一次抽奖活动。
小时,甲、乙二人在每个时段离场是等可能的。为吸引顾客,每个顾客可以参加一次抽奖活动。
(1) 用![]() 表示甲乙玩都不超过
表示甲乙玩都不超过![]() 小时的付费情况,求甲、乙二人付费之和为44元的概率;
小时的付费情况,求甲、乙二人付费之和为44元的概率;
(2)抽奖活动的规则是:顾客通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数![]() ,并按如右所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.
,并按如右所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.

【答案】(1)![]() (2)
(2)![]()
【解析】
试题(1)设甲付费a元,乙付费b元,其中a,b=10,18,26,34,由此利用列举法能求出“甲、乙二人付费之和为44元”的概率;(2)由已知0≤x≤1,0≤y≤1点(x,y)在正方形OABC内,作出条件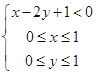 的区域,由此能求出顾客中奖的概率
的区域,由此能求出顾客中奖的概率
试题解析:(1)设甲付费![]() 元,乙付费
元,乙付费![]() 元,其中
元,其中![]() .
.
则甲、乙二人的费用构成的基本事件空间为:
![]()
![]()
![]() 共16种情形.
共16种情形.
其中,![]() 这
这![]() 种情形符合题意.
种情形符合题意.
故“甲、乙二人付费之和为![]() 元”的概率为
元”的概率为![]()
(2)由已知![]() 点
点![]() 如图的正方形
如图的正方形![]() 内,
内,
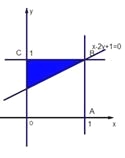
由条件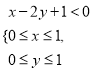
得到的区域为图中阴影部分
由![]() ,令
,令![]() 得
得![]() ;令
;令![]() 得
得![]() ;
;
由条件满足的区域面积![]() 。
。
设顾客中奖的事件为![]() ,则顾客中奖的概率
,则顾客中奖的概率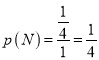

练习册系列答案
相关题目