题目内容
【题目】在四面体A-BCD中,有两条棱的长为![]()
![]() ,其余棱的长度都为1;
,其余棱的长度都为1;
(1)若![]() ,且
,且![]() ,求二面角A-BC-D的余弦值;
,求二面角A-BC-D的余弦值;
(2)求a的取值范围,使得这样的四面体是存在的;
【答案】(1)![]() ;(2)0<a
;(2)0<a![]() ;
;
【解析】
(1)由题意画出图形,作出二面角的平面角,利用余弦定理得答案;
(2)分两条长为a的棱相交与两条长为a的棱互为对棱分析,结合运动思想与极限思想求得每一种情况的a的范围,最后取并集得答案.
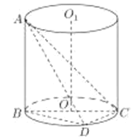
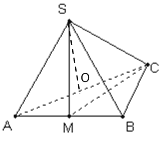
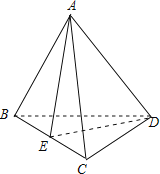
(1)如图,
过A作AE⊥BC,垂足为E,连接DE,则∠AED为二面角A﹣BC﹣D的平面角,
在等边三角形BCD中,∵BC=CD=BD=1,∴DE![]() ,
,
在等腰三角形ABC中,∵AB=AC![]() ,BC=1,∴AE
,BC=1,∴AE![]() .
.
在△AED中,由余弦定理得cos∠AED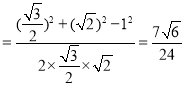 ;
;
(2)当两条长为a的棱相交时,不妨设AB=AC=a,AD=BD=CD=BC=1,
∵面ABC与平面BCD重合且A,D在BC异侧时,AE![]() ,此时AB=AC
,此时AB=AC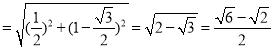 ,
,
面ABC与平面BCD重合且A,D在BC同侧时,AE=1![]() ,此时AB=AC
,此时AB=AC .
.
∴![]() ;
;
当两条长为a的棱互为对棱时,不妨设BC=AD=a,AB=AC=BD=CD=1,BC,AD可以无限趋近于0,
当ABCD为平面四边形时a![]() ,
,
∴0![]() .
.
综上,若四面体存在,则0<a![]() .
.

【题目】某网络营销部门为了统计某市网友某日在某淘宝店的网购情况,随机抽查了该市当天![]() 名网友的网购金额情况,得到如下统计表(如图).
名网友的网购金额情况,得到如下统计表(如图).
网购金额(单位:千元) | 频数 | 频率 |
| 3 | 0.05 |
|
|
|
| 9 | 0.15 |
| 15 | 0.25 |
| 18 | 0.30 |
|
|
|

若网购金额超过![]() 千元的顾客定义为“网购达人”,网购金额不超过
千元的顾客定义为“网购达人”,网购金额不超过![]() 千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为
千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为![]() .
.
(Ⅰ)试确定![]() 的值,并补全频率分布直方图(如图);
的值,并补全频率分布直方图(如图);
(Ⅱ)该营销部门为了进一步了解这![]() 名网友的购物体验,从“非网购达人”与“网购达人”中用分层抽样的方法抽取
名网友的购物体验,从“非网购达人”与“网购达人”中用分层抽样的方法抽取![]() 人,若需从这
人,若需从这![]() 人中随机选取
人中随机选取![]() 人进行问卷调查.设
人进行问卷调查.设![]() 为选取的
为选取的![]() 人中“网购达人”的人数,求
人中“网购达人”的人数,求![]() 的分布列及其数学期望.
的分布列及其数学期望.