题目内容
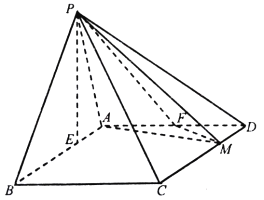
【题目】在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 点在底面
点在底面![]() 内的射影
内的射影![]() 在线段
在线段![]() 上,且
上,且![]() ,
, ![]() ,M在线段
,M在线段![]() 上,且
上,且![]() .
.
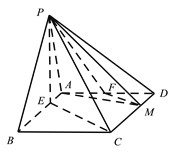
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)在线段AD上确定一点F,使得平面![]() 平面PAB,并求三棱锥
平面PAB,并求三棱锥![]() 的体积.
的体积.
【答案】(Ⅰ)见解析;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)根据余弦定理结合勾股定理可得![]() ,由
,由![]() 平面
平面![]() ,得
,得![]() 。从而由线面垂直的判定定理可得结果;(Ⅱ)取
。从而由线面垂直的判定定理可得结果;(Ⅱ)取![]() 是
是![]() 的中点,先证明
的中点,先证明![]() 平面
平面![]() ,即可证明
,即可证明![]() 平面
平面![]() ,然后根据棱锥的体积公式可得结果.
,然后根据棱锥的体积公式可得结果.
试题解析:(Ⅰ)证明:在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,由余弦定理得
,由余弦定理得![]() .
.
所以![]() ,从而有
,从而有![]() .
.
由![]() 平面
平面![]() ,得
,得![]() .
.
所以![]() 平面
平面![]() .
.
(Ⅱ)取![]() 是
是![]() 的中点,作
的中点,作![]() 交
交![]() 于点
于点![]() ,则四边形
,则四边形![]() 为平行四边形,
为平行四边形,
![]() ,则
,则![]() .
.
在![]() 中,
中, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,则
的中点,则![]() ,所以
,所以![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
![]() .
.
V = ![]() .
.
【方法点晴】本题主要考查线面垂直、面面垂直及棱锥的体积公式,属于中档题.证明直线和平面垂直的常用方法有:(1)利用直线和平面垂直的判定定理;(2)利用判定定理的推论![]() ;(3)利用面面平行的性质
;(3)利用面面平行的性质![]() ;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.
;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.

练习册系列答案
相关题目