题目内容
设函数f(x)在R上是偶函数,在区间(-∞,0)上递增,且f(2a2+a+1)<f(2a2-2a+3),求a的取值范围.
 .
.试题分析:由f(x)在R上是偶函数,在区间(-∞,0)上递增,
可知f(x)在(0,+∞)上递减.
∵2a2+a+1=
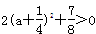 ,2a2-2a+3=
,2a2-2a+3= ,
,且f(2a2+a+1)<f(2a2-2a+3),∴2a2+a+1>2a2-2a+3,
即3a-2>0,解得
 .
.点评:典型题,抽象不等式求解问题,往往利用函数的奇偶性、单调性,将抽象不等式转化成具体不等式求解。在对称区间上,函数的奇偶性与单调性存在结论“奇同偶反”。

练习册系列答案
相关题目
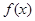 是定义在R上的奇函数,若对于x≥0,都有f(x+2)=
是定义在R上的奇函数,若对于x≥0,都有f(x+2)=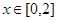 时,
时,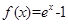 ,则
,则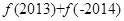 =
= 的图像关于点
的图像关于点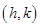 成中心对称,则函数
成中心对称,则函数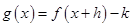 一定是( )
一定是( )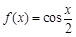 ,则下列等式成立的是
,则下列等式成立的是



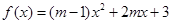 为偶函数,则m=
为偶函数,则m= 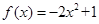 是偶函数,且在
是偶函数,且在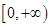 上是减少的。(13分)
上是减少的。(13分)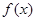 在R上的任一取值都有导数,且
在R上的任一取值都有导数,且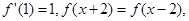 则曲线
则曲线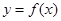 在
在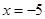 处的切线的斜率为 ( )
处的切线的斜率为 ( )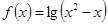 ,则f(-2)=
,则f(-2)=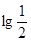
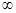 )(x
)(x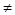 x),都有
x),都有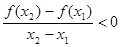 ,则
,则