题目内容
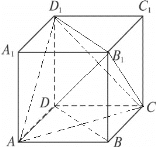
【题目】在正方体![]() 中,有下列结论:
中,有下列结论:
①![]() 平面
平面![]() ;
;
②异面直线AD与![]() 所成的角为
所成的角为![]() ;
;
③三棱柱![]() 的体积是三棱锥
的体积是三棱锥![]() 的体积的四倍;
的体积的四倍;
④在四面体![]() 中,分别连接三组对棱的中点的线段互相垂直平分.
中,分别连接三组对棱的中点的线段互相垂直平分.
其中正确的是________(填出所有正确结论的序号).
【答案】①④
【解析】
根据正方体的几何特征,证明线面平行,求异面直线夹角,求体积关系,分析正四面体对棱连线特点.
因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,故①正确;
,故①正确;
因为![]() ,所以异面直线AD与
,所以异面直线AD与![]() 所成的角等于
所成的角等于![]() ,在正方形
,在正方形![]() 中,
中,![]() ,故②错误;
,故②错误;
三棱柱![]() 的体积是三棱锥
的体积是三棱锥![]() 的体积的三倍,故③错误;
的体积的三倍,故③错误;
由正方体的性质可知,正方体三条对面中心连线线段相互垂直平分.
四面体![]() 是正四面体,其棱中点即正方体每个面的中心,对棱中点连线必经过正方体的中心,由对称性知,连接正四面体
是正四面体,其棱中点即正方体每个面的中心,对棱中点连线必经过正方体的中心,由对称性知,连接正四面体![]() 每组对棱中点的线段互相垂直平分,则④正确.
每组对棱中点的线段互相垂直平分,则④正确.
故答案为:①④

练习册系列答案
相关题目