题目内容
.(本小题满分16分)
数列 中,
中, ,
, ,且
,且 .
.
(1)求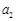 及
及 的通项公式;
的通项公式;
(2)设 是
是 中的任意一项,是否存在
中的任意一项,是否存在 ,使
,使 成等比数列?如存在,试分别写出
成等比数列?如存在,试分别写出 和
和 关于
关于 的一个表达式,并给出证明;
的一个表达式,并给出证明;
(3)证明:对一切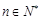 ,
, .
.
数列
 中,
中, ,
, ,且
,且 .
.(1)求
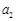 及
及 的通项公式;
的通项公式;(2)设
 是
是 中的任意一项,是否存在
中的任意一项,是否存在 ,使
,使 成等比数列?如存在,试分别写出
成等比数列?如存在,试分别写出 和
和 关于
关于 的一个表达式,并给出证明;
的一个表达式,并给出证明;(3)证明:对一切
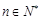 ,
, .
.解:(1)
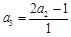 ,故
,故 . …………………1分
. …………………1分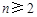 时,
时,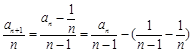
∴
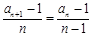 ,∴
,∴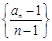 为常数列. ………………………4分
为常数列. ………………………4分∴
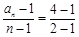 ,所以
,所以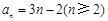 .
.又
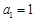 也满足上式,
也满足上式,∴
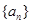 的通项公式为
的通项公式为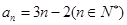 . ………………………6分
. ………………………6分(2)当
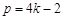 ,
, 时满足
时满足 成等比数列.
成等比数列.证明如下:
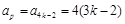 ,
,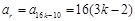 ,
,显然
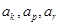 成等比数列. …………………………10分
成等比数列. …………………………10分(3)证明:
 时,
时, , …………………12分
, …………………12分∴当
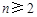 时,
时,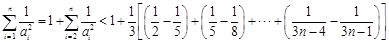
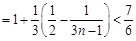 . …………………………15分
. …………………………15分又
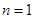 时,
时,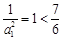 ,∴对一切
,∴对一切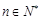 ,
,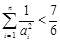 . …………………16分
. …………………16分略

练习册系列答案
相关题目
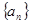 的通项公式
的通项公式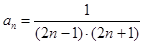 .若数列
.若数列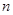 项和
项和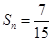 ,则
,则 的公差
的公差 ,它的前
,它的前 项和为
项和为 ,若
,若 ,且
,且 ,
, ,
,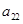 成等比数列.
成等比数列. 的前
的前 ,求证:
,求证: .
.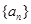 ,若点
,若点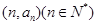 在经过点(5,3)的定直线
在经过点(5,3)的定直线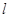 上,则数列
上,则数列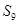 =( )
=( )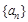 的首项
的首项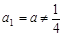 ,且
,且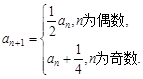
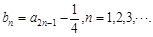
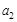 ,
,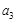 ;
;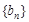 是否为等比数列,并证明你的结论.
是否为等比数列,并证明你的结论.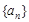 的通项公式.
的通项公式. 的前四项和为14,且
的前四项和为14,且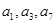 恰为等比数列
恰为等比数列 的前三项。
的前三项。 的前n项和
的前n项和
 为数列
为数列 的前n项和,若不等式
的前n项和,若不等式 对一切
对一切 恒成立,求实数
恒成立,求实数 的最小值。
的最小值。 的前n项和为
的前n项和为 ,正数数列
,正数数列 中
中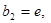
 )且
)且 总有
总有 是
是 的等差中项,
的等差中项, 的等比中项.
的等比中项. ;
;  .
. 中,
中, ,前n项和为
,前n项和为
 的前n项和为
的前n项和为 ,求满足不等式
,求满足不等式 的n值。
的n值。 满足
满足 ,则数列
,则数列 的前10项和为
的前10项和为


