Question

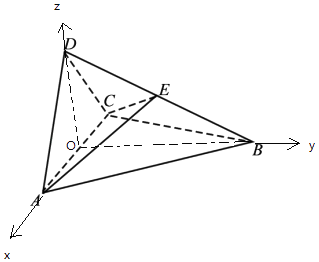
【题目】如图四面体ABCD中，△ABC是正三角形，AD=CD．（12分）
（1）证明：AC⊥BD；
（2）已知△ACD是直角三角形，AB=BD，若E为棱BD上与D不重合的点，且AE⊥EC，求四面体ABCE与四面体ACDE的体积比．

Answer 1

【答案】
（1）

证明：取AC中点O，连结DO、BO，

∵△ABC是正三角形，AD=CD，

∴DO⊥AC，BO⊥AC，

∵DO∩BO=O，∴AC⊥平面BDO，

∵BD平面BDO，∴AC⊥BD．

（2）

解：设AD=CD= ，则AC=AB=BC=BD=2，AO=CO=DO=1，

∴BO= = ，∴BO2+DO2=BD2，∴BO⊥DO，

以O为原点，OA为x轴，OB为y轴，OD为z轴，建立空间直角坐标系，

则C（﹣1，0，0），D（0，0，1），B（0， ，0），A（1，0，0），

设E（a，b，c）， ，（0≤λ≤1），则（a，b，c﹣1）=λ（0， ，﹣1），解得E（0， ，1﹣λ），

∴ =（1， ）， =（﹣1， ），

∵AE⊥EC，∴ =﹣1+3λ2+（1﹣λ）2=0，

由λ∈[0，1]，解得 ，∴DE=BE，

∵四面体ABCE与四面体ACDE的高都是点A到平面BCD的高h，

∵DE=BE，∴S△DCE=S△BCE，

∴四面体ABCE与四面体ACDE的体积比为1．

【解析】（1.）取AC中点O，连结DO、BO，推导出DO⊥AC，BO⊥AC，从而AC⊥平面BDO，由此能证明AC⊥BD．
（2.）设AD=CD= ，则AC=AB=BC=BD=2，AO=CO=DO=1，BO= ，推导出BO⊥DO，以O为原点，OA为x轴，OB为y轴，OD为z轴，建立空间直角坐标系，由AE⊥EC，求出DE=BE，由此能求出四面体ABCE与四面体ACDE的体积比．