题目内容
(本小题满分12分)
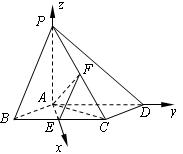
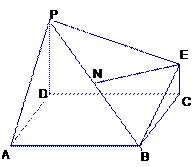
如图,已知四棱锥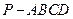 ,底面
,底面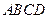 为菱形,
为菱形,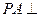 平面
平面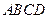 ,
,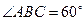 ,
,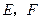 分别是
分别是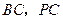 的中点.
的中点.
(Ⅰ)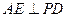 判定AE与PD是否垂直,并说明理由
判定AE与PD是否垂直,并说明理由
(Ⅱ)若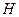 为
为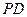 上的动点,
上的动点,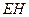 与平面
与平面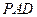 所成最大角的正切值为
所成最大角的正切值为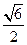 ,求二面角
,求二面角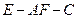 的余弦值。
的余弦值。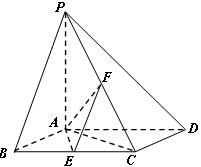
如图,已知四棱锥
 ,底面
,底面 为菱形,
为菱形, 平面
平面 ,
, ,
,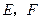 分别是
分别是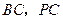 的中点.
的中点.(Ⅰ)
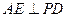 判定AE与PD是否垂直,并说明理由
判定AE与PD是否垂直,并说明理由(Ⅱ)若
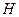 为
为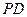 上的动点,
上的动点,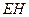 与平面
与平面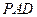 所成最大角的正切值为
所成最大角的正切值为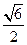 ,求二面角
,求二面角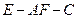 的余弦值。
的余弦值。
(Ⅰ)垂直.证明:由四边形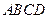 为菱形,
为菱形,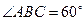 ,可得
,可得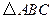 为正三角形.
为正三角形.
因为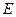 为
为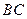 的中点,所以
的中点,所以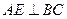 .又
.又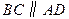 ,因此
,因此 .
.
因为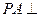 平面
平面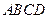 ,
,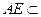 平面
平面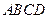 ,所以
,所以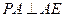 .
.
而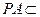 平面
平面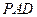 ,
,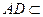 平面
平面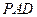 且
且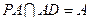 ,
,
所以 平面
平面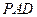 .又
.又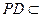 平面
平面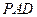 ,所以
,所以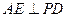 .
.
(Ⅱ)解:设 ,
, 为
为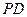 上任意一点,连接
上任意一点,连接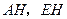 .
.
 由(Ⅰ)知
由(Ⅰ)知 平面
平面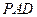 ,则
,则 为
为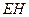 与平面
与平面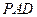 所成的角.
所成的角.
在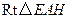 中,
中,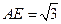 ,所以当
,所以当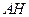 最短时,
最短时, 最大,
最大,
即当 时,
时, 最大.
最大.
此时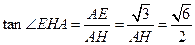 ,
,
因此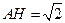 .又
.又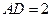 ,所以
,所以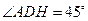 , 高#考#资#源#
, 高#考#资#源#
所以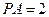 .
.
解法一:因为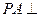 平面
平面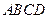 ,
,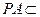 平面
平面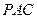 ,
,
所以平面 平面
平面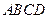 .过
.过 作
作
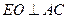 于
于 ,则
,则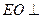 平面
平面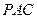 ,
,
过 作
作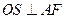 于
于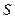 ,连接
,连接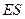 ,则
,则 为二面角
为二面角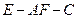 的平面角,
的平面角,
在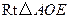 中,
中, ,
,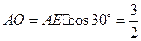 ,
,
又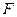 是
是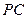 的中点,在
的中点,在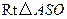 中,
中,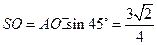 ,
,
又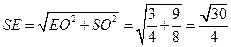 ,在
,在 中,
中,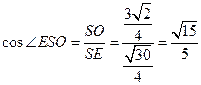 ,
,
即所求二面角的余弦值为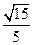 .
.
解法二:由(Ⅰ)知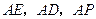 两两垂直,以
两两垂直,以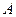 为坐标原点,建立
为坐标原点,建立 如图所示的空间直角坐标系,又
如图所示的空间直角坐标系,又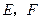 分别为
分别为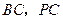 的中点,
的中点,
∴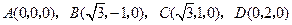 ,
,
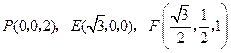 ,
,
所以 .
.
设平面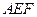 的一法向量为
的一法向量为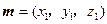 ,则
,则
因此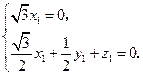 取
取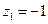 ,则
,则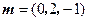 ,
,
因为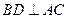 ,
,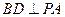 ,
,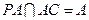 ,
,
所以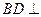 平面
平面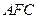 ,故
,故 为平面
为平面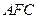 的一法向量.
的一法向量.
又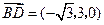 ,所以
,所以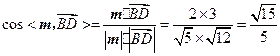 .
.
因为二面角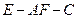 为锐角,所以所求二面角的余弦值为
为锐角,所以所求二面角的余弦值为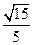 .
.
 为菱形,
为菱形, ,可得
,可得 为正三角形.
为正三角形.
因为
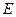 为
为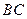 的中点,所以
的中点,所以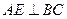 .又
.又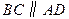 ,因此
,因此 .
.因为
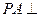 平面
平面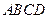 ,
,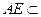 平面
平面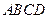 ,所以
,所以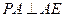 .
.而
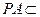 平面
平面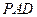 ,
,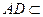 平面
平面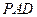 且
且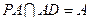 ,
,所以
 平面
平面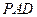 .又
.又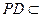 平面
平面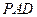 ,所以
,所以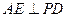 .
.(Ⅱ)解:设
 ,
,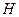 为
为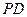 上任意一点,连接
上任意一点,连接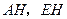 .
. 由(Ⅰ)知
由(Ⅰ)知 平面
平面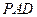 ,则
,则 为
为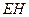 与平面
与平面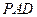 所成的角.
所成的角.在
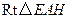 中,
中,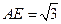 ,所以当
,所以当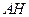 最短时,
最短时, 最大,
最大,即当
 时,
时, 最大.
最大.此时
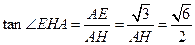 ,
,因此
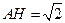 .又
.又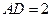 ,所以
,所以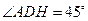 , 高#考#资#源#
, 高#考#资#源#所以
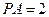 .
. 解法一:因为
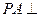 平面
平面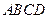 ,
,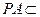 平面
平面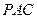 ,
,所以平面
 平面
平面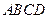 .过
.过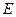 作
作
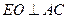 于
于 ,则
,则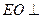 平面
平面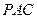 ,
,过
 作
作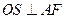 于
于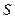 ,连接
,连接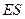 ,则
,则 为二面角
为二面角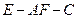 的平面角,
的平面角,在
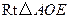 中,
中, ,
,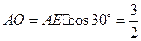 ,
,又
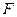 是
是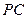 的中点,在
的中点,在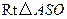 中,
中,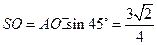 ,
,又
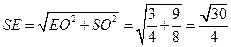 ,在
,在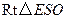 中,
中,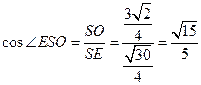 ,
,即所求二面角的余弦值为
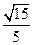 .
.解法二:由(Ⅰ)知
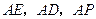 两两垂直,以
两两垂直,以 为坐标原点,建立
为坐标原点,建立 如图所示的空间直角坐标系,又
如图所示的空间直角坐标系,又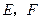 分别为
分别为 的中点,
的中点,∴
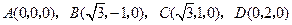 ,
,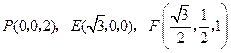 ,
,所以
 .
.设平面
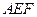 的一法向量为
的一法向量为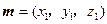 ,则
,则
因此
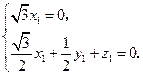 取
取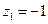 ,则
,则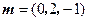 ,
,因为
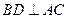 ,
,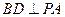 ,
,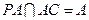 ,
,所以
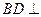 平面
平面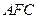 ,故
,故 为平面
为平面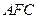 的一法向量.
的一法向量.又
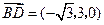 ,所以
,所以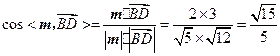 .
.因为二面角
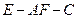 为锐角,所以所求二面角的余弦值为
为锐角,所以所求二面角的余弦值为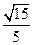 .
.略

练习册系列答案
相关题目
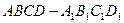 中,
中,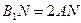 ,
,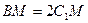
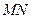 的长度。(12分)
的长度。(12分)
 E为PC的中点,AD=CD=l,BC=PC,
E为PC的中点,AD=CD=l,BC=PC,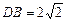
 ,底面三角形
,底面三角形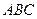 为正三角形,侧棱
为正三角形,侧棱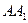
 底面
底面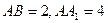 ,
,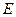 为
为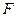 为
为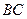 中点.
中点.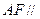 平面
平面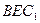 ;
;
 杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?请用你的计算数据说明理由。
杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?请用你的计算数据说明理由。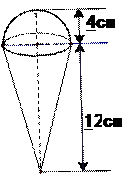
 平面
平面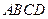 ,
,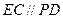 ,
,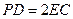 ,
, 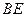 //平面
//平面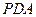 ;
;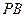 的中点,求证:
的中点,求证: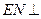 平面
平面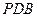 ;
;
 与
与 都是边长为
都是边长为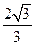 的等边三角形,且平面
的等边三角形,且平面 平面
平面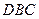 ,过点
,过点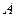 作
作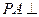 平面
平面 ,且
,且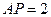 .
.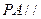 平面
平面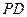 与平面
与平面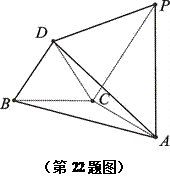
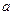 平行于平面
平行于平面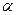 ,直线
,直线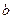 在平面
在平面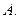 平行
平行 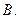 异面
异面  平行或异面
平行或异面  平行、相交或异面
平行、相交或异面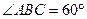 ,点M
,点M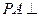 平面ABCD,AC、BD交于点O。
平面ABCD,AC、BD交于点O。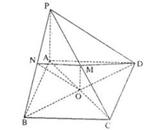
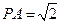 ,求证:AM
,求证:AM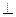 平面PBD;
平面PBD;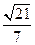 ,求PA的长
,求PA的长