题目内容
7.已知四边形ABCD是边长为6的正方形,E为AB的中点,点F在BC上,且BF:FC=2:1,AF与EC相交于点P,求四边形APCD的面积.分析 取BF的中点M,连接EM,可得S△CPF=$\frac{1}{4}$S△CEM,由S△CBE=9,M、F是BC的三等分点,可得S△CEM=6,解得S△CPF=1.5,而S△ABF=12,从而可求S四边形APCD=S正方形ABCD-S△ABF-S△CPF的值.
解答 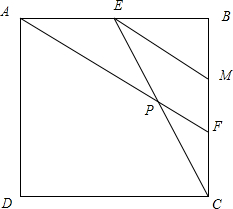 解:取BF的中点M,连接EM,
解:取BF的中点M,连接EM,
因为E是AB的中点,
所以EM是△ABF的中位线,
所以EM∥AF,
所以△CPF∽△CEM,
因为BF:FC=2:1,
所以F是CM的中点,
所以$\frac{CF}{CM}=\frac{1}{2}$,
所以$\frac{{S}_{△CPF}}{{S}_{△CEM}}=\frac{1}{4}$,即S△CPF=$\frac{1}{4}$S△CEM,
因为S△CBE=9,M、F是BC的三等分点,
所以S△CEM=6,
所以S△CPF=1.5,
而S△ABF=12,
所以S四边形APCD=S正方形ABCD-S△ABF-S△CPF
=36-12-1.5
=22.5.
点评 本题主要考查了相似三角形的性质,三角形面积公式,三角形中位线的性质的应用,属于基本知识的考查.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
19.下列各式中,能成立的是( )
| A. | log3(6-4)=log36-log34 | B. | log3(6-4)=$\frac{lo{g}_{3}6}{lo{g}_{3}4}$ | ||
| C. | log35-log36=$\frac{lo{g}_{3}5}{lo{g}_{3}6}$ | D. | log23+log210=log25+log26 |
17.f(cosx)=cos2x,则f(sin30°)=( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | -1 | D. | -$\frac{1}{2}$ |