题目内容
3．已知函数y=loga（x+c）（a＞0且a≠1，a，c为常数）的图象如图，则下列结论正确的是（ ）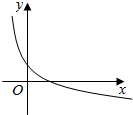
| A． | a＞0，c＞1 | B． | a＞1，0＜c＜1 | C． | 0＜a＜1，0＜c＜1 | D． | 0＜a＜1，c＞1 |
分析 根据函数的单调性，可判断a的取值，根据函数图象与坐标轴的交点位置，可判断c的取值，进而得到答案．
解答 解：∵函数y=loga（x+c）（a＞0且a≠1，a，c为常数）为减函数，
故0＜a＜1，
∵函数图象与x轴的交点在正半轴，
故x=1-c＞0，即c＜1，
∵函数图象与y轴有交点，
故c＞0，
故0＜c＜1，
故选：C．
点评 本题考查的知识点是对数函数的图象和性质，熟练掌握对数函数的图象和性质，是解答的关键．
练习册系列答案
相关题目
13．若一个四棱锥的底面是边长为4的正方形，各侧棱都等于3，那么这个四棱锥的高等于（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | 5 | D． | $\sqrt{7}$ |
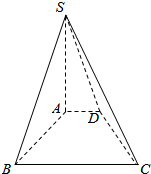已知四棱锥S-ABCD中，底面ABCD是直角梯形，∠ABC=90°，AD∥BC，SA=AB=BC=2，AD=1，SA⊥底面ABCD．