题目内容
15.在△ABC中,内角A,B,C对应的边分别为a,b,c(a≤b≤c),且bcosC+ccosB=2asinA.(Ⅰ)求角A;
(Ⅱ)求证:${a^2}≥(2-\sqrt{3})bc$;
(Ⅲ)若a=b,且BC边上的中线AM长为$\sqrt{7}$,求△ABC的面积.
分析 (Ⅰ)已知等式利用正弦定理化简,利用两角和与差的正弦函数公式及二倍角的正弦函数公式化简,再利用诱导公式化简求出sinA的值,即可确定出A的度数;
(Ⅱ)表示出所证不等式左右两边之差,利用余弦定理及完全平方公式性质化简,判断差的正负即可得证;
(Ⅲ)由a=b,得到A=B,求出C的度数,在三角形AMC中,由AM的长与cosC的值,求出AC的长,利用三角形面积公式求出三角形ABC面积即可.
解答 解:(Ⅰ)∵bcosC+ccosB=2asinA,
∴sinBcosC+sinCcosB=2sinAsinA,
即sin(B+C)=2sinAsinA?sinA=2sinAsinA,
∵sinA>0,∴sinA=$\frac{1}{2}$,
∵a≤b≤c,
∴0<A≤$\frac{π}{3}$,
∴A=$\frac{π}{6}$;
(Ⅱ)∵a2-(2-$\sqrt{3}$)bc=b2+c2-2bccos$\frac{π}{6}$-(2-$\sqrt{3}$)bc=b2+c2-2bc=(b-c)2≥0,
∴a2≥(2-$\sqrt{3}$)bc;
(Ⅲ)由a=b及(Ⅰ)知A=B=$\frac{π}{6}$,
∴C=$\frac{2π}{3}$,
设AC=x,则MC=$\frac{1}{2}$x,
又AM=$\sqrt{7}$,
在△AMC中,由余弦定理得AC2+MC2-2AC•MCcosC=AM2,
即x2+($\frac{x}{2}$)2-2x•$\frac{x}{2}$•cos120°=7,
解得:x=2,
则S△ABC=$\frac{1}{2}$x2sin$\frac{2π}{3}$=$\sqrt{3}$.
点评 此题考查了余弦定理,两角和与差的正弦函数,以及三角形面积公式,熟练掌握定理及公式是解本题的关键.

| A. | {1,4} | B. | {1,4,6} | C. | {2,4,6} | D. | {1,2,4,6} |
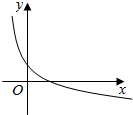
| A. | a>0,c>1 | B. | a>1,0<c<1 | C. | 0<a<1,0<c<1 | D. | 0<a<1,c>1 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $\frac{32\sqrt{15}}{15}$,$\frac{8\sqrt{15}}{5}$,$\frac{16\sqrt{15}}{15}$ | B. | $\frac{32}{15}$,$\frac{8}{5}$,$\frac{16}{15}$ | ||
| C. | 4,3,2 | D. | 8,6,4 |
